题目描述

在 JOI 王国，有 $N$ 个岛屿，编号从 $1$ 到 $N$。每个岛屿都有一个不安全等级。岛屿 $i\ (1 \le i \le N)$ 的不安全等级是 $S_i$。

在 JOI 王国，岛屿之间的船只是主要的交通方式。有 $M$ 艘船，编号从 $1$ 到 $M$。船 $j\ (1 \le j \le M)$ 连接岛屿 $A_j$ 和岛屿 $B_j$。我们可以在需要时运行船只。可以通过多次乘船从任何岛屿到达其他岛屿。

在 JOI 王国，有计划引入新的船只。我们可以选择任何一对岛屿来连接新引入的船只。

有一天，发生了一起事件。一艘停泊的船遭到了攻击。JOI 王国的总理 K 决定引入新的船只。他还要求 JOI 王国的船只满足以下安全条件。

• 当船停泊在岛屿 $i\ (1 \le i \le N)$ 时，船上的保安人数必须大于或等于 $S_i$。

然而，由于雇佣保安很昂贵，我们希望最小化雇佣保安的人数。只要满足“可以通过多次乘船从任何岛屿到达其他岛屿”的条件，就可以废除当前运行的船只。

因此，我们将按如下方式运行船只。这里，$k$ 是新引入的船只数量。

1. 对于每艘新引入的船，我们选择它连接的两个岛屿。
2. 我们选择若干（大于或等于 $0$）船只，并废除它们。允许废除新引入的船只。
3. 对于每艘船，我们将其停泊在它连接的两个岛屿之一。我们让若干保安登船。此外，必须满足以下条件。

条件 对于每对岛屿 $u, v\ (1 \le u \le N, 1 \le v \le N)$，可以通过多次重复以下操作将乘客从岛屿 $u$ 运输到岛屿 $v$。在此过程中，安全条件必须始终得到满足。

• 我们让乘客或保安登上停泊在乘客或保安所在岛屿的船。
• 我们让乘客或保安在船当前停泊的岛屿下船。
• 我们将船从当前停泊的岛屿移动到船连接的另一个岛屿。

由于预算有限，我们最多可以引入 $Q$ 艘新船。对于每个 $k\ (0 \le k \le Q)$，总理 K 想知道如果新引入的船只数量为 $k$ 时，雇佣保安的最小可能人数。

编写一个程序，给定岛屿的信息、船只的航线以及我们可以引入的新船数量，计算每个 $k$ 的雇佣保安的最小可能人数。

输入格式

从标准输入读取以下数据。

$N\ M\ Q$

$S_1\ S_2\ \cdots\ S_N$

$A_1\ B_1$

$A_2\ B_2$

$\vdots$

$A_M\ B_M$

输出格式

向标准输出写入 $Q+1$ 行。输出的第 $(k+1)$ 行 $(0 \le k \le Q)$ 应包含如果新引入的船只数量为 $k$ 时雇佣保安的最小可能人数。

4 3 0
2 1 3 2
1 2
2 3
3 4

7

4 3 1
2 1 3 2
1 2
2 3
3 4

7
5

3 3 0
1 1 1
1 2
1 3
2 3

2

8 7 0
2 2 2 2 2 2 2 2
1 2
2 3
3 4
4 5
5 6
6 7
7 8

14

8 7 0
16 39 36 23 15 48 23 56
1 2
1 3
2 4
2 5
3 6
3 7
7 8

245

10 13 4
314 159 265 358 979 323 846 264 338 327
1 2
1 4
2 3
2 5
3 6
4 5
4 7
5 6
5 8
6 9
7 8
8 9
9 10

3139
2901
2722
2567
2461

提示

【样例解释 #1】

如果新引入的船只数量为 $0$，我们需要 $7$ 名保安。例如，如果我们按如下方式分配船只和 $7$ 名保安，则条件得到满足。

• 船 $1$ 最初停泊在岛屿 $2$，并有两名保安登上船 $1$。
• 船 $2$ 最初停泊在岛屿 $2$，并有两名保安登上船 $2$。
• 船 $3$ 最初停泊在岛屿 $4$，并有三名保安登上船 $3$。

让我们解释如何在以下两种情况下运输乘客。

• 我们将乘客从岛屿 $1$ 运输到岛屿 $4$。
• 我们将乘客从岛屿 $3$ 运输到岛屿 $2$。

我们可以按如下方式将乘客从岛屿 $1$ 运输到岛屿 $4$。船 $1, 2, 3$ 停泊的岛屿，以及船 $1, 2, 3$ 上的保安人数按此顺序写出。岛屿 $1, 2, 3, 4$ 上的保安人数按此顺序写出。

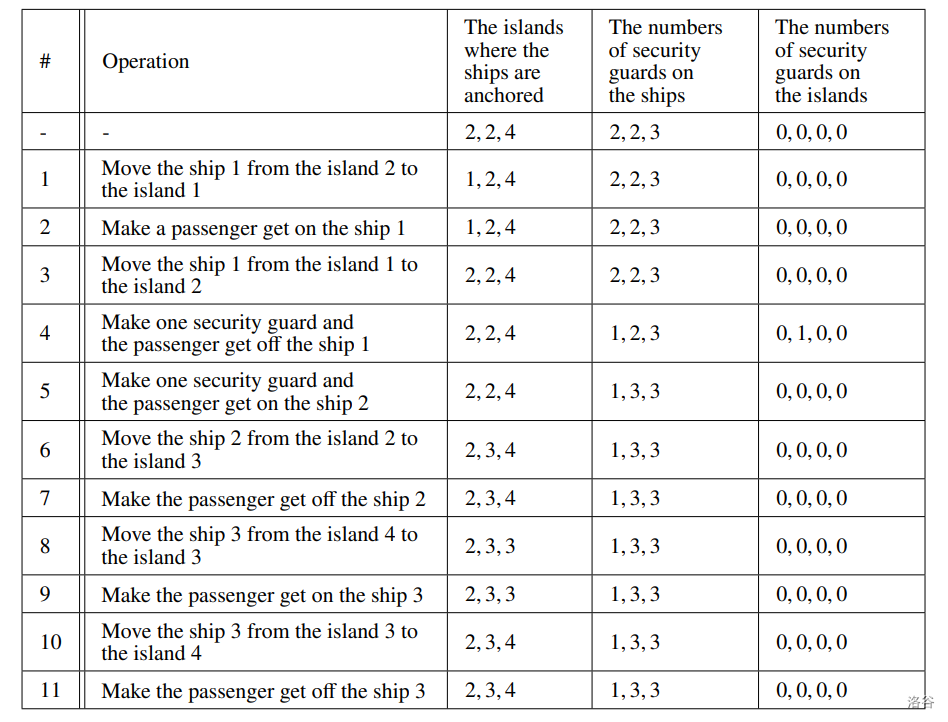
我们可以按如下方式将乘客从岛屿 $3$ 运输到岛屿 $2$。

由于如果保安人数小于或等于 $6$，则无法满足条件，因此输出 $7$。

此样例输入满足子任务 $2, 3, 4, 5, 6, 7$ 的约束。

【样例解释 #2】

如果新引入的船只数量为 $0$，与样例输入 $1$ 类似，我们需要 $7$ 名保安。

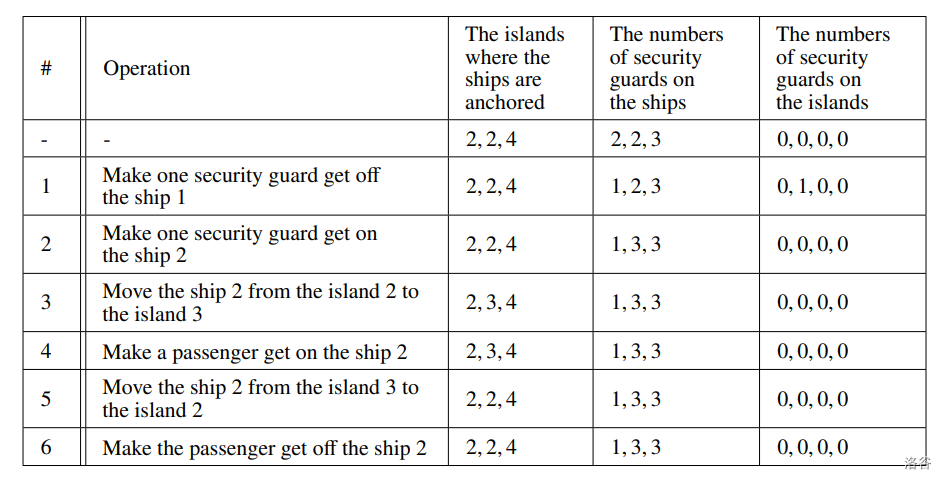
如果新引入的船只数量为 $1$，我们需要 $5$ 名保安。例如，如果我们按如下方式分配船只和 $5$ 名保安，则条件得到满足。

• 我们引入一艘连接岛屿 $2$ 和岛屿 $4$ 的新船。（在下文中，我们称之为船 $4$。）
• 我们废除船 $3$。
• 我们最初将船 $1$ 停泊在岛屿 $2$，并让两名保安登上船 $1$。
• 我们最初将船 $2$ 停泊在岛屿 $2$，并让一名保安登上船 $2$。
• 我们最初将船 $4$ 停泊在岛屿 $2$，并让两名保安登上船 $4$。

此样例输入满足子任务 $5, 6, 7$ 的约束。

【样例解释 #3】

如果新引入的船只数量为 $0$，我们需要 $2$ 名保安。例如，如果我们按如下方式分配船只和 $2$ 名保安，则条件得到满足。

• 我们废除船 $3$。
• 我们最初将船 $1$ 停泊在岛屿 $1$，并让一名保安登上船 $1$。
• 我们最初将船 $2$ 停泊在岛屿 $1$，并让一名保安登上船 $2$。

此样例输入满足子任务 $4, 5, 6, 7$ 的约束。

【样例解释 #4】

此样例输入满足所有子任务的约束。

【样例解释 #5】

此样例输入满足子任务 $3, 4, 5, 6, 7$ 的约束。

【样例解释 #6】

此样例输入满足子任务 $5, 6, 7$ 的约束。

【数据范围】

对于所有测试数据，满足：

• $2 \le N \le 2\times 10 ^ 5$；
• $N - 1 \le M \le 4\times 10 ^ 5$；
• $0 \le Q \le 2\times 10 ^ 5$；
• $1 \le S_i \le 10 ^ 9\ (1 \le i \le N)$；
• $1 \le A_j < B_j \le N\ (1 \le j \le M)$；
• $(A_x, B_x) \neq (A_y, B_y)\ (1 \le x < y \le M)$；
• 可以通过多次乘船从任何岛屿到达其他岛屿；
• 给定值均为整数。

子任务编号	分值	特殊限制
$1$	$12$	$M = N - 1$，$Q = 0$，$S_i \le 2\ (1 \le i \le N)$，$A_j = j$，$B_j = j + 1\ (1 \le j \le M)$
$2$	$13$	$M = N - 1$，$Q = 0$，$A_j = j$，$B_j = j + 1\ (1 \le j \le M)$
$3$	$12$	$M = N - 1$，$Q = 0$
$4$	$13$	$Q = 0$
$5$	$8$	$N \le 16$
$6$	$18$	$N \le 3 000$
$7$	$24$	无

题面翻译由 ChatGPT-4o 提供。