题目描述

:::align{center}

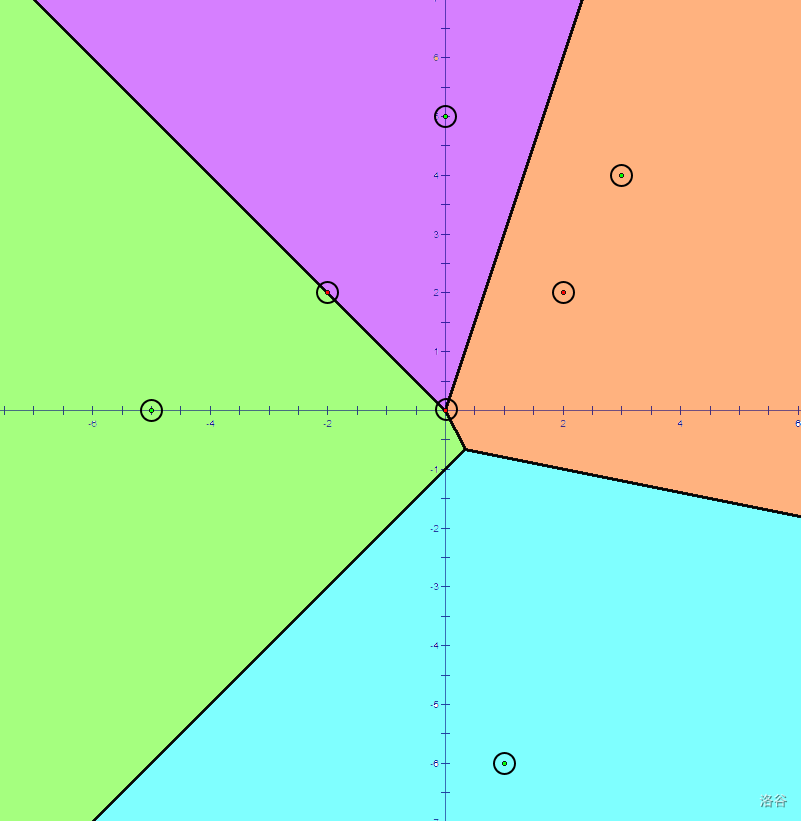
Voronoi Diagram of size 4. :::

In the 2-dimensional Cartesian coordinate system, we define the $\textbf{Voronoi Diagram}$ of a non-empty set of points $S$, as a diagram that divides the plane by the criteria "which point in the set $S$ is closest in this location?". More precisely, the Voronoi diagram of a given non-empty point set $\{P_1, P_2, \cdots, P_n\}$ is a collection of $\textbf{regions}$: A point $K$ is included in region $i$ if and only if $d(P_i, K) \le d(P_j, K)$ holds for all $1 \le j \le n$, where $d(X, Y)$ denotes the Euclidean distance between point $X$ and $Y$.

For example, in the picture above, every location over the plane is colored by the closest point with such location. The points which belongs to a single region is colored by a light color indicating a region, and the points which belongs to more than one region forms lines and points colored black.

There is an algorithm which computes the Voronoi Diagram in $O(n \log(n))$, but it is infamous to be very complicated and hard. In fact, we are lenient problem setters, so we set $n \leq 2000$, which means you can solve this task with slower Voronoi Diagram algorithms!

In this task, you should solve the $\textbf{point query problem}$ in Voronoi diagram: in the Voronoi diagram constructed with the set of points $\{P_1, P_2, \cdots, P_n\}$, you should determine which region(s) the point belongs in. More precisely, you will be given $q$ queries of points. For each query point, you should determine the following:

• If it's not included in any region, output $\texttt{NONE}$.
• If it's included in exactly one region, output $\texttt{REGION X}$, where $\texttt{X}$ is the index of such region.
• If it's included in exactly two regions, output $\texttt{LINE X Y}$, where $\texttt{X}$ and $\texttt{Y}$ ($\texttt{X}$ $<$ $\texttt{Y}$) are the indices of such two regions.
• If it's included in three or more regions, output $\texttt{POINT}$.

输入格式

In the first line, the number of points consisting Voronoi diagram $n$, and the number of queries $q$ are given. ($3 \le n \le 2\ 000, 1 \le q \le 250\ 000$)

In the $i$th line of next $n$ lines, two integers indicating $x$ and $y$ co-ordinate of $P_i$ are given. These are the points consisting the Voronoi diagram. All $n$ points are distinct. ($|x|, |y| \le 10^4$)

In the $j$th line of next $q$ lines, two integers indicating $x$ and $y$ co-ordinate of $Q_j$ are given. For each point $Q_j$, you should determine in which region(s) the given point belongs to. ($|x|, |y| \le 10^4$)

输出格式

Output consists of $q$ lines. In the $j$th line, you should print one of following:

• If $Q_j$ is not included in any region, output $\texttt{NONE}$.
• If $Q_j$ is included in exactly one region, output $\texttt{REGION X}$, where $\texttt{X}$ is the index of such region.
• If $Q_j$ is included in exactly two regions, output $\texttt{LINE X Y}$, where $\texttt{X}$ and $\texttt{Y}$ ($\texttt{X}$ $<$ $\texttt{Y}$) are the indices of such two regions.
• If $Q_j$ is included in three or more regions, output $\texttt{POINT}$.

4 3
-5 0
0 5
3 4
1 -6
-2 2
0 0
2 2

LINE 1 2
POINT
REGION 3

提示

Example is illustrated as diagram above.