题目描述

$\textbf{Tree}$ is a recursive structure, which is either:

• $\textbf{Empty}$. Empty tree is denoted as $-1$ and has a size of 0.
• $\textbf{Non-empty}$. Non-empty tree $T$ is denoted as a pair of two trees $(T_1, T_2)$, where $T_1$ is called $\textbf{left subtree}$ of $T$, and $T_2$ is called $\textbf{right subtree}$ of $T$. If $T = (-1, -1)$, then we call such $T$ a $\textbf{leaf}$. Leaf has a size of 1, and non-leaf has a size of $|T_1| + |T_2|$, where $|T_1|$ is the size of $T_1$, and $|T_2|$ is the size of $T_2$.

A non-empty tree $T$ is a $\textbf{Fake Plastic Tree}$, if the tree is $\textit{balanced}$. Formally, Let $T = (T_1, T_2)$. If $|T_1| = |T_2|$ or $|T_1| = |T_2| + 1$ holds, then $T$ is a Fake Plastic Tree.

In computer science, trees are commonly used as a data structure, and they are stored in a memory. At first, there are no trees in the memory, and only an imaginary $\textit{null pointer}$ exists (which corresponds to empty tree, $-1$). You can allocate a tree in the memory, by setting $T_1$ and $T_2$ as either a null pointer or a pointer of an existing tree. Then, the memory is extended by adding $T = (T_1, T_2)$ into its structure. Note that pointer can be described as a small integer, reducing the need for explicitly storing the whole tree.

Formally, memory $M$ is an inductive structure, which at first contains only empty tree $-1$. ($M = \{-1\}$). You can expand the memory with following operation $M \leftarrow M \cup \{(T_1, T_2)\}$, where $T_1 \in M, T_2 \in M$. If a tree $T$ is inserted in $i$-th stage, then it has the $\textbf{index}$ $i-1$. For a tree with index $i$, their subtrees can be represented as a pair of integer in range $[-1, i-1]$.

Your task is to construct a memory $M$, which satisfies the following:

• Every tree in $M$ is either empty or Fake Plastic Tree.
• $M$ has at most 125 non-empty trees.
• There exists a tree $T \in M$, where $|T| = N$ holds. $N$ is an integer, and is given as an input.

输入格式

The first line contains a single integer $T$, the number of test cases. ($1 \leq T \leq 2000$)

In the next $T$ lines, a single integer $N$ is given, which indicates the number of leaves your tree should contain. ($1 \leq N \leq 10^{18}$)

输出格式

For each case, you should print $V + 2$ lines, where $V$ is the number of non-empty trees in $M$. ($1 \leq V \leq 125$).

In the first line, you should print single integer $V$.

In the next $V$ lines, you should print two space-separated integer $L_i, R_i$, which indicates the index of left subtree and right subtree for a tree with index $i$. ($-1 \leq L_i, R_i \leq i - 1$).

In the $V+2$-th line, you should print $P$, the index of the tree which contains $N$ nodes. ($0 \leq P \leq V-1$).

It is guaranteed that an answer always exists under the given condition.

4
1
2
3
4

1
-1 -1
0
3
-1 -1
-1 -1
0 1
2
3
-1 -1
0 0
1 0
2
5
-1 -1
0 0
0 0
2 1
1 2
3

提示

:::align{center}

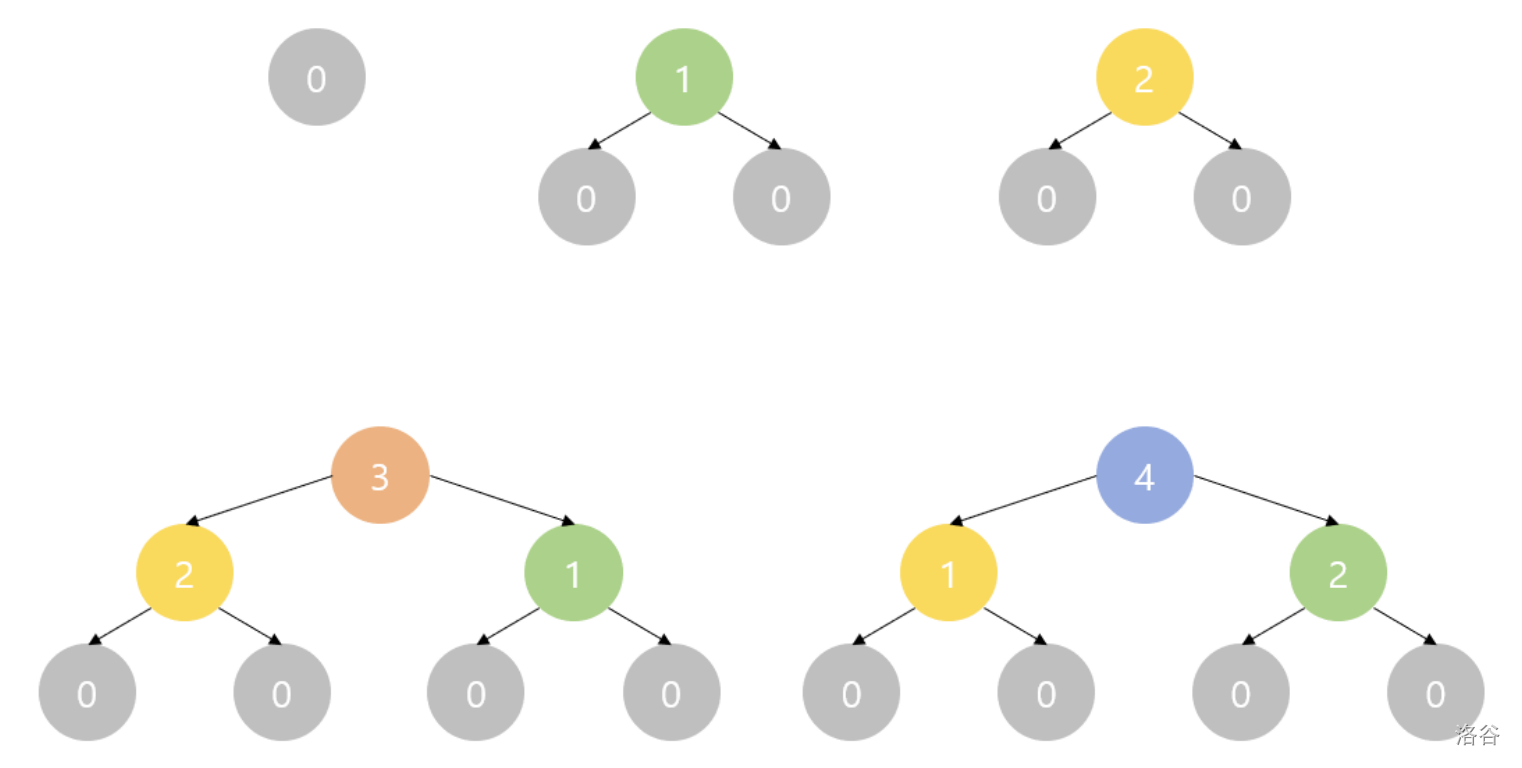
Illustration of output for $N = 4$ in the example. :::