题目描述

Chalk has been actively traveling the world with his friends taking pictures in all the coolest places. Most recently, he made his way to Europe, where he studied the history of napkin folding. Ever since, Chalk has been collecting a wide variety of napkins to practice the art of napkin folding.

Chalk's napkins can be defined as simple polygons. A simple polygon is a polygon in which no edges intersect except for adjacent edges which meet at their shared vertex. Each vertex of the polygon is on exactly two edges.

Chalk folds his napkins by first drawing a folding pattern on them. A folding pattern is a set of $\mathbf{K}-1$ line segments which are drawn on the napkin. Each line segment connects two points with rational coordinates on the border of the polygon defining the napkin and is fully contained in the polygon. No two line segments in a folding pattern may touch or overlap, except possibly at common endpoints. A folding pattern of $\mathbf{K}-1$ line segments splits the napkin into $\mathbf{K}$ polygonal regions. Two points are in the same region if there exists some continuous line (not necessarily straight) between them which does not intersect any edge of the polygon or any line segment in the folding pattern — even at endpoints.

Chalk is only interested in neat folding patterns. A folding pattern is neat if any two regions that are adjacent to the same folding line segment $F$ are symmetric with respect to $F$. This means that folding the napkin along that line segment would result in the two regions lining up perfectly.

The following picture illustrates a neat folding pattern with $\mathbf{K}=8$ regions.

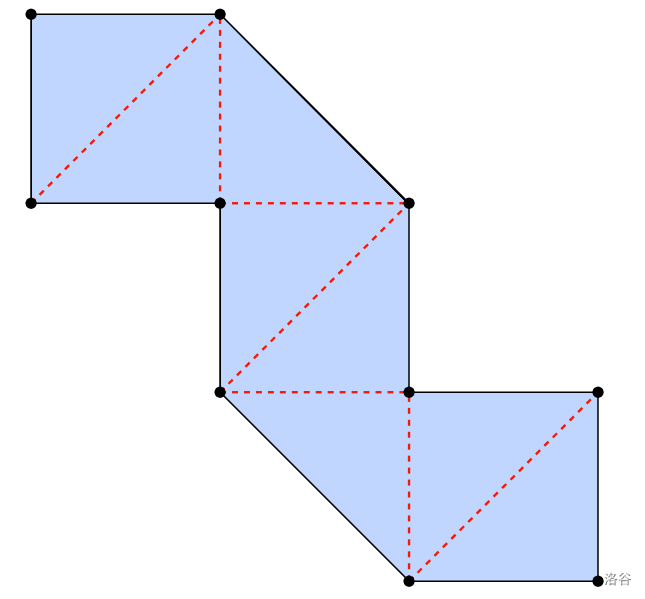
Chalk has been successfully folding his collection of napkins using neat folding patterns. But he has some napkins in his collection that he has not been able to find a neat folding pattern for. For each of those napkins, Chalk needs your help to find a neat folding pattern with $\mathbf{K}$ regions or determine that no such neat folding pattern exists.

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case starts with a line containing two integers $\mathbf{N}$ and $\mathbf{K}$: the number of points in the polygon defining Chalk's napkin and the number of regions to split the napkin into with a neat folding pattern containing $\mathbf{K}-1$ line segments.

The polygon defining the napkin is represented as a list of the $\mathbf{N}$ vertices, as encountered when traveling along the perimeter of the polygon in the clockwise direction, with the first vertex being chosen arbitrarily. The next $\mathbf{N}$ lines represent that list. The $\mathbf{i}$-th of these contains two integers $\mathbf{X}_{\mathbf{i}}$ and $\mathbf{Y}_{\mathbf{i}}$, indicating that the $\mathbf{i}$-th point is located at $(\mathbf{X}_{\mathbf{i}}, \mathbf{Y}_{\mathbf{i}})$ in two-dimensional space.

输出格式

For each test case, output one line containing Case #$x$: $y$, where $x$ is the test case number (starting from 1) and $y$ is POSSIBLE if it is possible to make a neat folding pattern with $\mathbf{K}$ regions and IMPOSSIBLE otherwise.

If it is possible to make a neat folding pattern with $\mathbf{K}$ regions, output $\mathbf{K}-1$ more lines listing the segments of a neat folding pattern with $\mathbf{K}$ regions, in any order. Each line should represent a different segment as $\mathbf{A}_{\mathbf{x}}$ $\mathbf{A}_{\mathbf{y}}$ $\mathbf{B}_{\mathbf{x}}$ $\mathbf{B}_{\mathbf{y}}$, where $(\mathbf{A}_{\mathbf{x}}, \mathbf{A}_{\mathbf{y}})$ and $(\mathbf{B}_{\mathbf{x}}, \mathbf{B}_{\mathbf{y}})$ are the two endpoints of the segment, in any order. Each of $\mathbf{A}_{\mathbf{x}}$, $\mathbf{A}_{\mathbf{y}}$, $\mathbf{B}_{\mathbf{x}}$, and $\mathbf{B}_{\mathbf{y}}$ should be in the form $\mathbf{N}/\mathbf{D}$ where $\mathbf{N}$ and $\mathbf{D}$ are positive integers (written with no leading zeroes) sharing no common prime factors, and representing the rational number $\mathbf{N}/\mathbf{D}$. There must be no whitespace between $\mathbf{N}$ and /, or between / and $\mathbf{D}$.

4
4 2
1 1
1 2
2 2
2 1
3 2
1 1
1 2
2 1
8 2
1 3
3 5
5 5
4 4
7 3
5 1
4 2
3 1
8 2
1 3
3 5
4 4
5 5
7 3
5 1
4 2
3 1

Case #1: POSSIBLE
1/1 2/1 2/1 1/1
Case #2: POSSIBLE
1/1 1/1 3/2 3/2
Case #3: IMPOSSIBLE
Case #4: POSSIBLE
1/1 3/1 7/1 3/1

1
10 8
4 1
3 1
2 2
2 3
1 3
1 4
2 4
3 3
3 2
4 2

Case #1: POSSIBLE
3/1 1/1 4/1 2/1
3/1 1/1 3/1 2/1
2/1 2/1 3/1 2/1
2/1 2/1 3/1 3/1
2/1 3/1 3/1 3/1
2/1 3/1 2/1 4/1
1/1 3/1 2/1 4/1

提示

Sample Explanation

Note: Sample 2 is not valid for Test set 1. Only Sample 1 will be tested prior to running Test set 1 (the same way samples normally are). Moreover, Sample 2 will not be tested prior to running Test set 2.

For Sample Case #1, a neat folding pattern with $\mathbf{K}=2$ can be drawn using any of the 4 dashed lines:

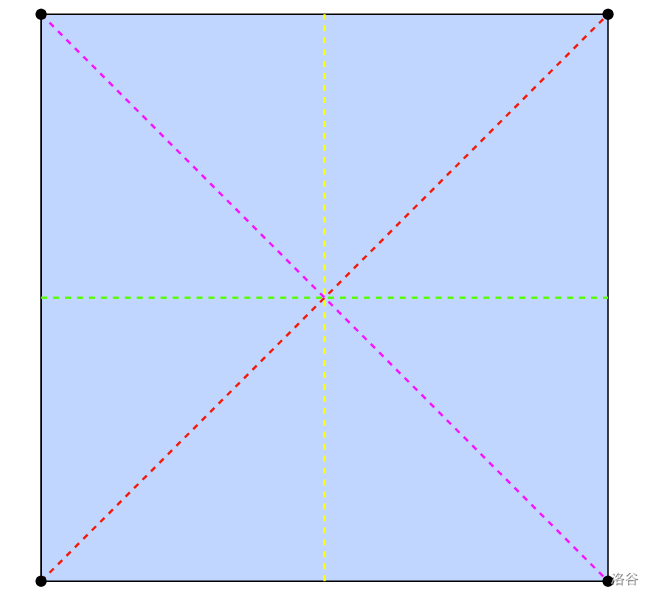
For Sample Case #2, a neat folding pattern with $\mathbf{K}=2$ can be drawn as follows:

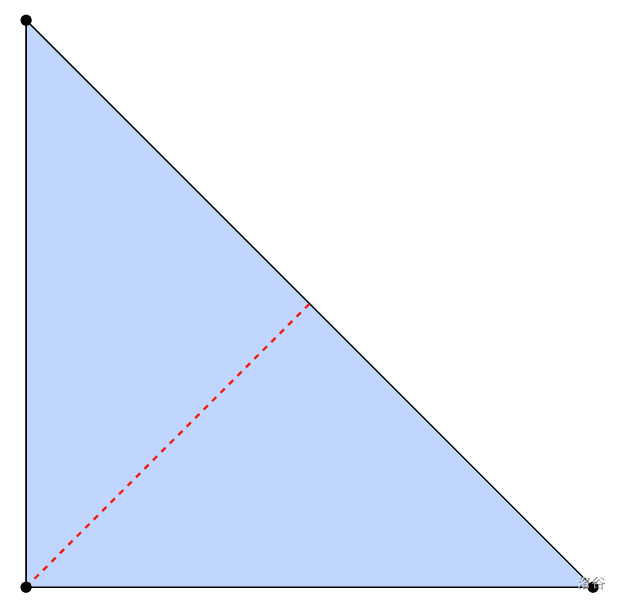
For Sample Case #3, there are no neat folding patterns:

For Sample Case #4, there are two possible neat folding patterns with $\mathbf{K}=2$:

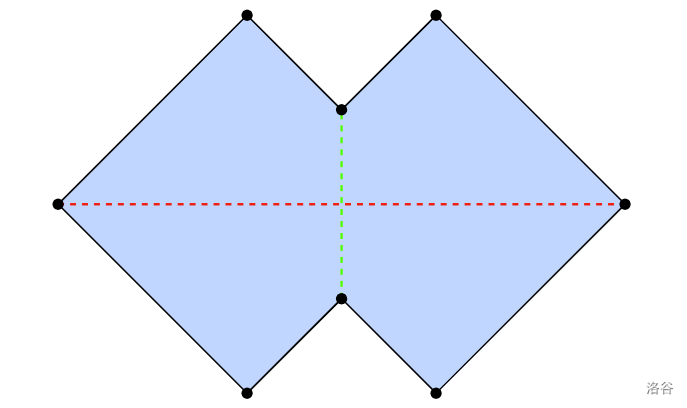
For the test set 2 sample case, a neat folding pattern with $\mathbf{K}=8$ can be drawn as follows:

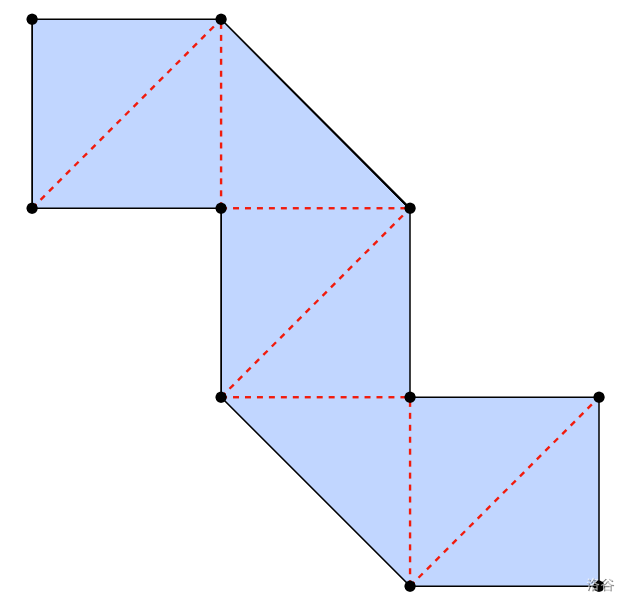
Limits

• $1 \leq \mathbf{T} \leq 100$.
• $3 \leq \mathbf{N} \leq 200$.
• $1 \leq \mathbf{X}_{\mathbf{i}} \leq 1000$, for all $\mathbf{i}$.
• $1 \leq \mathbf{Y}_{\mathbf{i}} \leq 1000$, for all $\mathbf{i}$.
• The $\mathbf{N}$ points are given in clockwise order.
• No two adjacent edges of the polygon are collinear.
• The polygon is a simple polygon with strictly positive area.
• No two edges intersect except for adjacent edges at their shared endpoint.

Test set 1 (4 Pts, Visible)

• $\mathbf{K}=2$.

Test set 2 (39 Pts, Hidden)

• $2 \leq \mathbf{K} \leq 10$.