题目背景

这是问题的 24bit 版本。本题与 68bit 版本和 16bit[v] 版本的区别在于此版本中电路的位长 $w=24$。此外，16bit[v] 版本和本题的另一个区别是本题的电路中 LSH 与 RSH 的右操作数必须是字面量。

题目描述

本题为提交答案题。

以下是简要题面，关于其中名词的详细定义见后文（有些名词可能和你所见过的定义并不完全相符）。

定义所有长度为 $\bm4$ 的排列组成的集合为 $\mathcal P$，$w=\color{blue}24$ 是位长，$B$ 是 $[0,2^w)$ 内的整数组成的集合。

你需要设计一个函数 $f:\mathcal P\to B$ 和一个电路 $C:(B, B)\to B$，使得对于任意 $p,q\in\mathcal P$ 都有：

$$\operatorname{cyc}(p\circ q)=C(f(p),f(q))$$

其中 $\circ$ 是排列的复合，$\operatorname{cyc}(\cdot)$ 表示排列的置换环个数。

电路 $C$ 中涉及到的运算门个数不能超过 $10^4$，得分将根据电路 $C$ 中的运算门个数评定，得分计算方式见说明 / 提示部分。

---

以下是可能涉及到的定义：

关于排列

一个长度为 $n$ 的排列是元素为 $1$ 到 $n$ 中互不重复的整数的长度为 $n$ 的序列。两个排列 $p,q$ 的复合 $(p\circ q)_i=p_{q_i}$。对于一个排列 $p$，集合 $S$ 是其置换环当且仅当 $S$ 是极小的满足 $S=\{p_x\mid x\in S\}$ 的集合。$\operatorname{cyc}(p)$ 是排列 $p$ 的置换环个数。

一个排列 $p$ 的排名是字典序不大于它的排列个数，关于字典序的定义选手可以自行搜索。

关于电路

在一个电路 $C$ 中，你有 $100$ 个变量 $x_{1\dots 100}$ 可供使用，其中 $x_1,x_2$ 是输入信号接收 $C$ 的两个参数，$x_3$ 是输出信号在电路运行完毕后作为 $C$ 的返回值传出。初始除了 $x_1,x_2$ 每个变量的值都是 $0$。每个变量都是 $B$ 内的整数，并且运算时随时保持对 $2^w$ 取模。你可以认为电路中的变量都是 $w$ 位的自然溢出的无符号整数。

一个数值有以下两种表达（后将值为 $p$ 的数值记作 #p，不带 # 的字母表示普通变量）：

• i，表示变量 $x_i$。
• N n，表示十进制字面量 $n$，其中 $0\le n<2^w$。

电路由若干计算门组成，所有计算门按顺序依次进行。计算门分以下七种：

• i AND #p #q，令 $x_i\gets p\land q$，其中 $\land$ 是按位与运算。
• i OR #p #q，令 $x_i\gets p\lor q$，其中 $\lor$ 是按位或运算。
• i XOR #p #q，令 $x_i\gets p\oplus q$，其中 $\oplus$ 是按位异或运算。
• i NOT #p，令 $x_i\gets \lnot p$，其中 $\lnot$ 是按位取反运算。
• i LSH #p #q，令 $x_i\gets p\cdot 2^q$，其中要求 $\bm{q<w}$ 且 $\bm q$ 必须是字面量。
• i RSH #p #q，令 $x_i\gets \lfloor\frac p{2^q}\rfloor$，其中要求 $\bm{q<w}$ 且 $\bm q$ 必须是字面量。
• i POPCNT #p，令 $x_i\gets\operatorname{popcount}(p)$，其中 $\operatorname{popcount}(\cdot)$ 表示二进制中一的个数。

关于各类位运算的详细定义，选手可以自行搜索。

输入格式

没有任何输入。

输出格式

你可以选择提交答案的生成器代码，或者直接提交答案。如果想要直接提交答案的话需要把答案文件压缩到一个 zip 文件内并使用提交文件方式提交。

首先 $24$ 行，第 $i$ 行一个 $[0,2^w)$ 内的整数 $x$ 表示排名为 $i$ 的排列 $p$ 的 $f$ 值 $f(p)=x$。

接下来一行一个非负整数 $L$，表示电路涉及到的计算门个数。

接下来 $L$ 行，每行描述一个计算门。

1
2
4
8
16
32
64
128
256
512
1024
2048
4096
8192
16384
32768
65536
131072
262144
524288
1048576
2097152
4194304
8388608
3
3 XOR 1 2
3 OR 3 N 7
3 POPCNT 3

提示

样例解释

样例仅供演示输出格式，并没有实际意义，也不能在本题得到任何分数。

样例输出中的电路 $C$ 描述了 $C(x,y)=\operatorname{popcount}((x\oplus y)\lor7)$。

电路模拟

我们在下发文件中提供了一个可以计算电路的运行结果的 C++ 代码 compiler.cpp（需要以至少 C++ 11 标准运行），选手可以使用 compiler.cpp 辅助理解电路的运行模式。

注意：compiler.cpp 仅对合法的输入有效，对不合法的输入的运行结果不做任何保证。

评分标准

若你的输出出现下列情况，那么该测试点不得分：

• $\operatorname{cyc}(p\circ q)\neq C(f(p),f(q))$。
• 电路 $C$ 不合法（使用标号不在 $[1,100]$ 内的变量 / 字面量的值 $\ge2^w$ / 出现无法识别或不合法的语句 / 使用超过 $10^4$ 个运算门 / 运算门参数不合法）。

否则若你使用了 $c$ 个运算门，那么你的得分为：

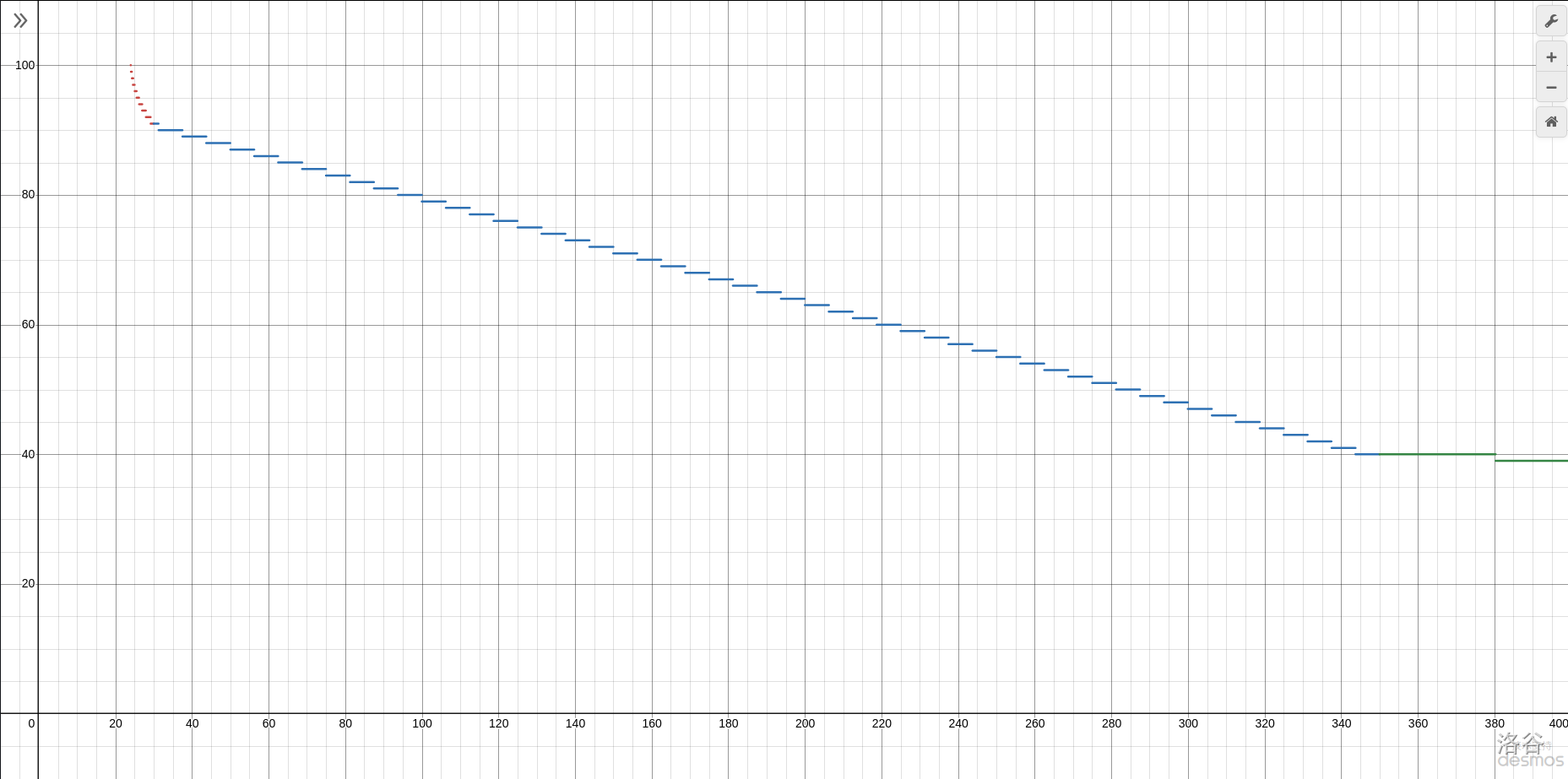
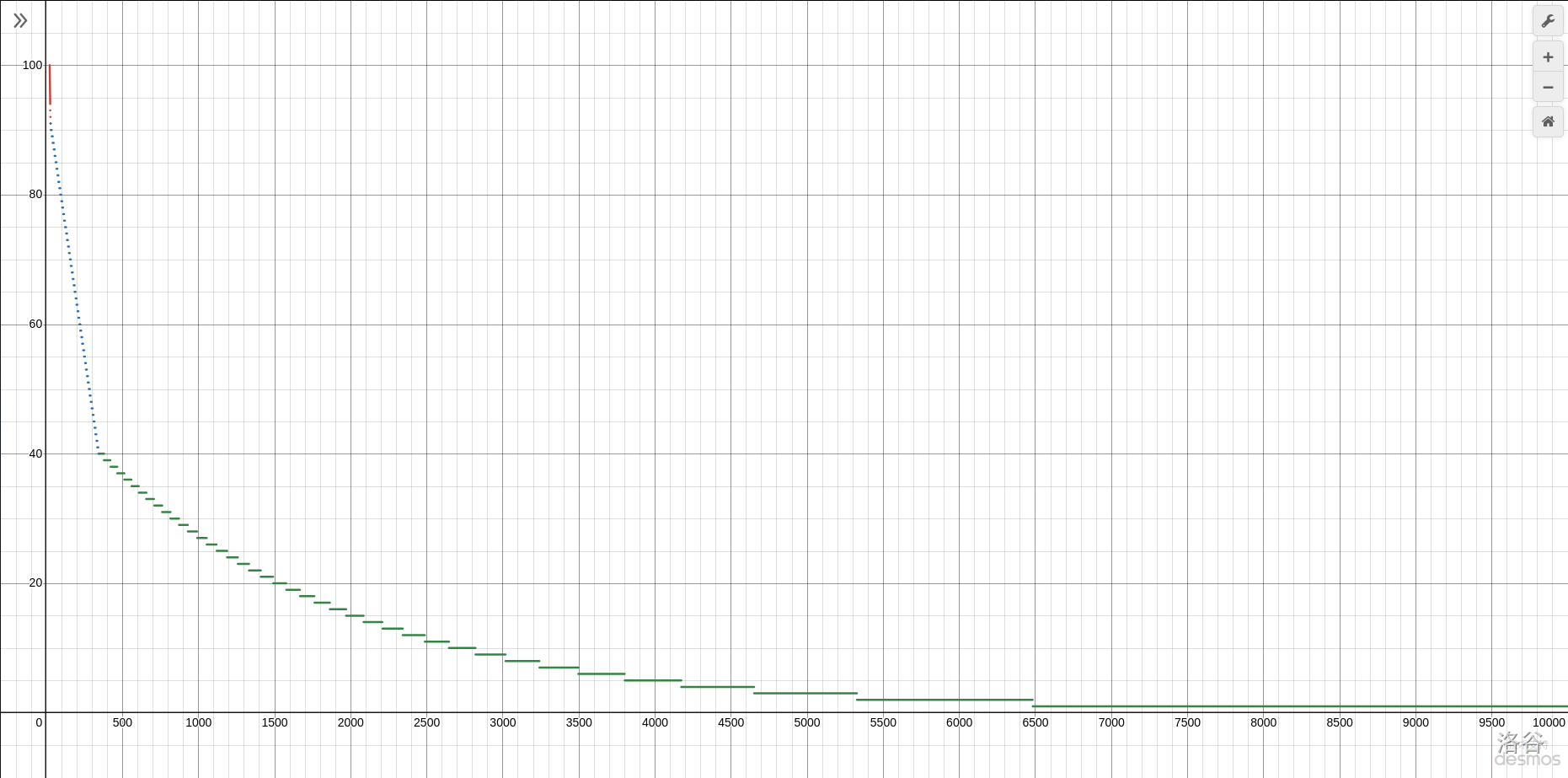
$$\mathrm{score}=\begin{cases}100&c\le 24\\\left\lfloor15.25\log_{30}\left(\frac{0.09}{c-23}\right)+111\right\rfloor&24<c\le30\\\left\lceil-0.16c+95\right\rceil&30<c\le350\\\left\lceil49\cdot0.9994^{c}\right\rceil&35010^4\end{cases} $$

下表为在一些特殊的 $c$ 中选手在该测试点得到的分数：

$c$	$\mathrm{score}$	$c$	$\mathrm{score}$
$10^4$	$1$	$300$	$47$
$6000$	$2$	$200$	$63$
$5000$	$3$	$100$	$79$
$3000$	$9$	$80$	$83$
$2000$	$15$	$50$	$87$
$1000$	$27$	$30$	$91$
$700$	$33$	$25$	$97$
$500$	$37$	$24$	$100$

这里给出 $c>24$ 时两张得分函数缩放不同的图像，以供参考（由 desmos 提供）。