题目背景

译自 NOISG 2017 B.Roadside Advertisements。

NOISG2017 拥有 $5$ 个赞助商。

题目描述

新加坡的地图可以视为一张 $V$ 个点 $V-1$ 条边的图，其中点的编号为 $0,1,\cdots V-1$。保证任意两点间有且仅有唯一路径。

已知 $5$ 个赞助商分别位于 $a,b,c,d,e$ 号点，NOISG 主席 TAN Sun-Teck 想要在一些边上投放广告，使得 $5$ 个赞助商两两间的最短路径上都投放了至少一则广告。

对于每条边，在该边上投放广告的成本是已知的。投放广告的总成本是每条需投放广告的道路成本的总和。$Q$ 次询问，每次给定 $a,b,c,d,e$，求满足要求的最低总成本。

输入格式

第一行一个正整数 $V$。

接下来 $V−1$ 行，每行三个整数 $u,v,w$，表示 $u$ 号点和 $v$ 号点间有一条道路相连，并且在这条道路上投放广告需要 $w$ 新加坡元。

接下来一行包含一个正整数 $Q$，表示询问次数。

接下来 $Q$ 行，每行五个整数 $a,b,c,d,e$，表示 $5$ 个赞助商的位置。保证 $a,b,c,d,e$ 两两不同。

输出格式

对于每次询问，一行一个整数表示投放广告的最低总成本。

5
0 1 1
1 2 2
2 3 3
3 4 4
1
4 0 3 1 2

10

6
4 0 4
0 1 2
1 3 9
3 5 1
3 2 5
2
4 0 3 5 2
0 4 1 3 5

21
16

提示

【样例 2 解释】

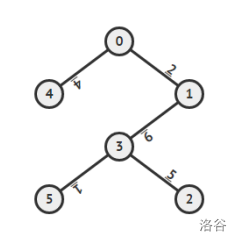
对于第一次询问，$5$ 个赞助商分别位于 $4,0,3,5,2$ 号点（请注意编号不一定按升序排列）。易知我们需要在每一条路边投放广告，最低成本是所有道路的成本之和，即 $4+2+9+1+5=21$。

对于第二次询问，$5$ 个赞助商位于 $0,4,1,3,5$ 号点。这一次我们不需要在 $(3,2)$ 这条道路上投放广告。因此总成本为 $21−5=16$。

【数据范围】

本题采用 $\text{Subtask}$ 捆绑测试。

特殊性质：保证每个点最多与 $2$ 个点间有道路相连。

对于所有数据，保证 $5\le V\le5\times10^4$，$1\le Q\le 10^4$，$0\le u,v<V$ 且 $1\le w\le1000$。