题目描述

This problem is about finding the distance between two nodes of a strictly binary tree. Oh, is that too easy?! Ok, the tree is potentially infinite now. Keep it up and we will start going up the aleph numbers.

In this problem, a tree is either a single node $X$, or a node $X$ with two trees attached to it: a left subtree and a right subtree. In both cases, $X$ is the root of the tree. If the tree is not a single node, the roots of both the left and right subtrees are the only children of $X$.

There is a set of colors numbered from 0 to $\mathbf{N}$, inclusive. Each node is of exactly one color. There might be zero, one, or multiple nodes of each color. Each node of color 0 (white) is a leaf node (that is, it has no children). Each node of color $i$, for $1 \leq i \leq \mathbf{N}$, has exactly 2 children: the left one is color $\mathbf{L}_{i}$ and the right one is color $\mathbf{R}_{i}$. The root of the tree is color 1 (black). Note that the tree may have a finite or countably infinite number of nodes.

For example, the following picture illustrates a finite tree defined by the lists $\mathbf{L}=[3,0,0]$ and $\mathbf{R}=[2,0,2]$. Color 2 is blue and color 3 is yellow.

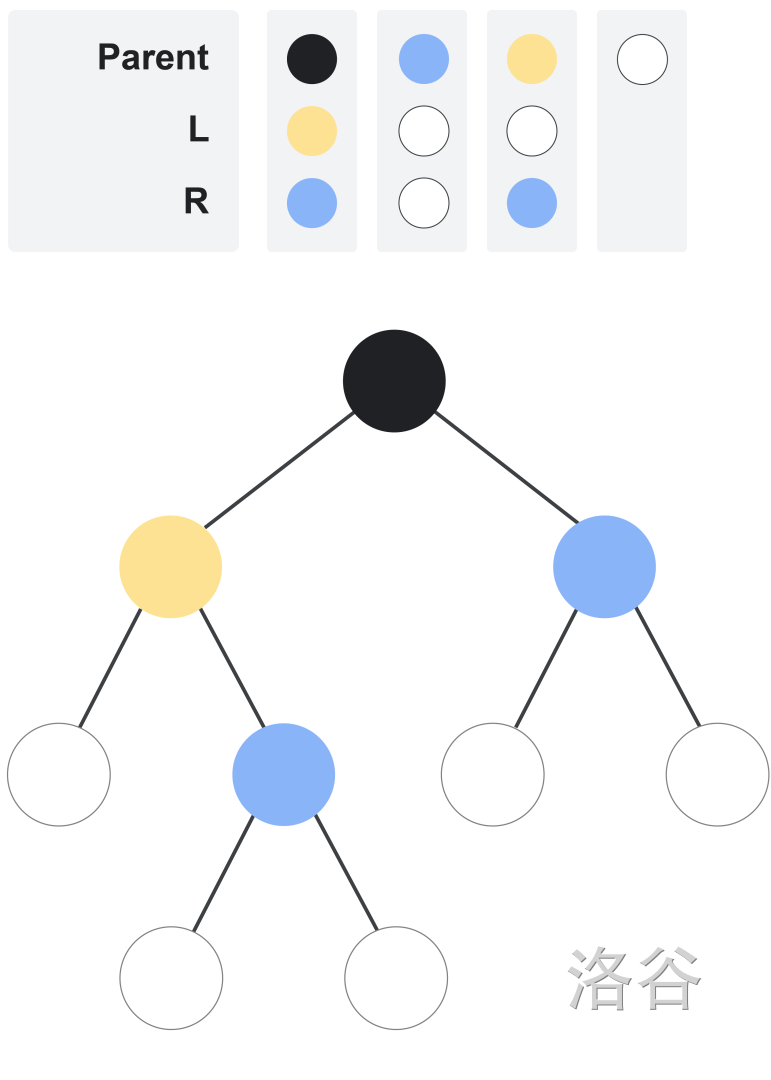
The distance between two nodes in the tree is the minimum number of steps that are needed to get from one node to the other. A step is a move from a node to its direct parent or its direct child.

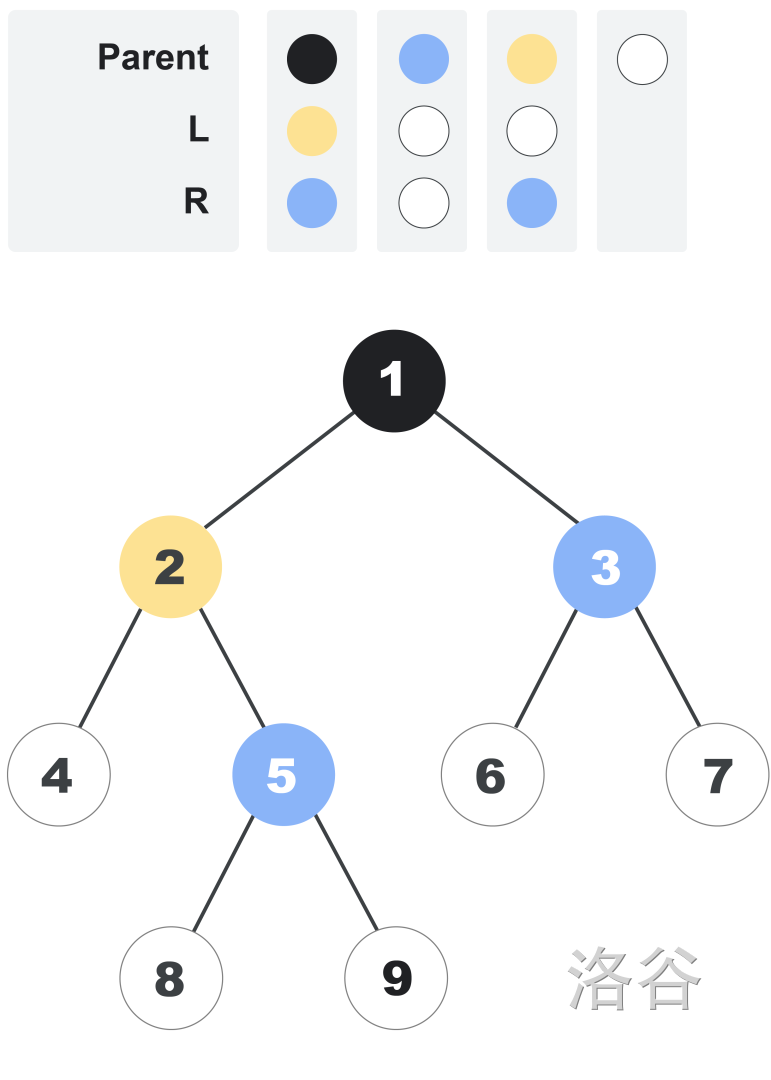
Nodes in the tree are indexed using positive integers. The root has index $1$. Then, other nodes are indexed using consecutive integers, with nodes with smaller distances to the root being indexed first. For nodes that are equidistant to the root, nodes that are further to the left are indexed first. For example, the following picture adds indices to each node in the tree we presented before. Notice that each node's index is independent from its color.

As another example, the following picture shows the first $33$ nodes of an infinite tree defined by the lists $\mathbf{L}=[3,4,2,4]$ and $\mathbf{R}=[2,2,4,0]$. Color $4$ is green.

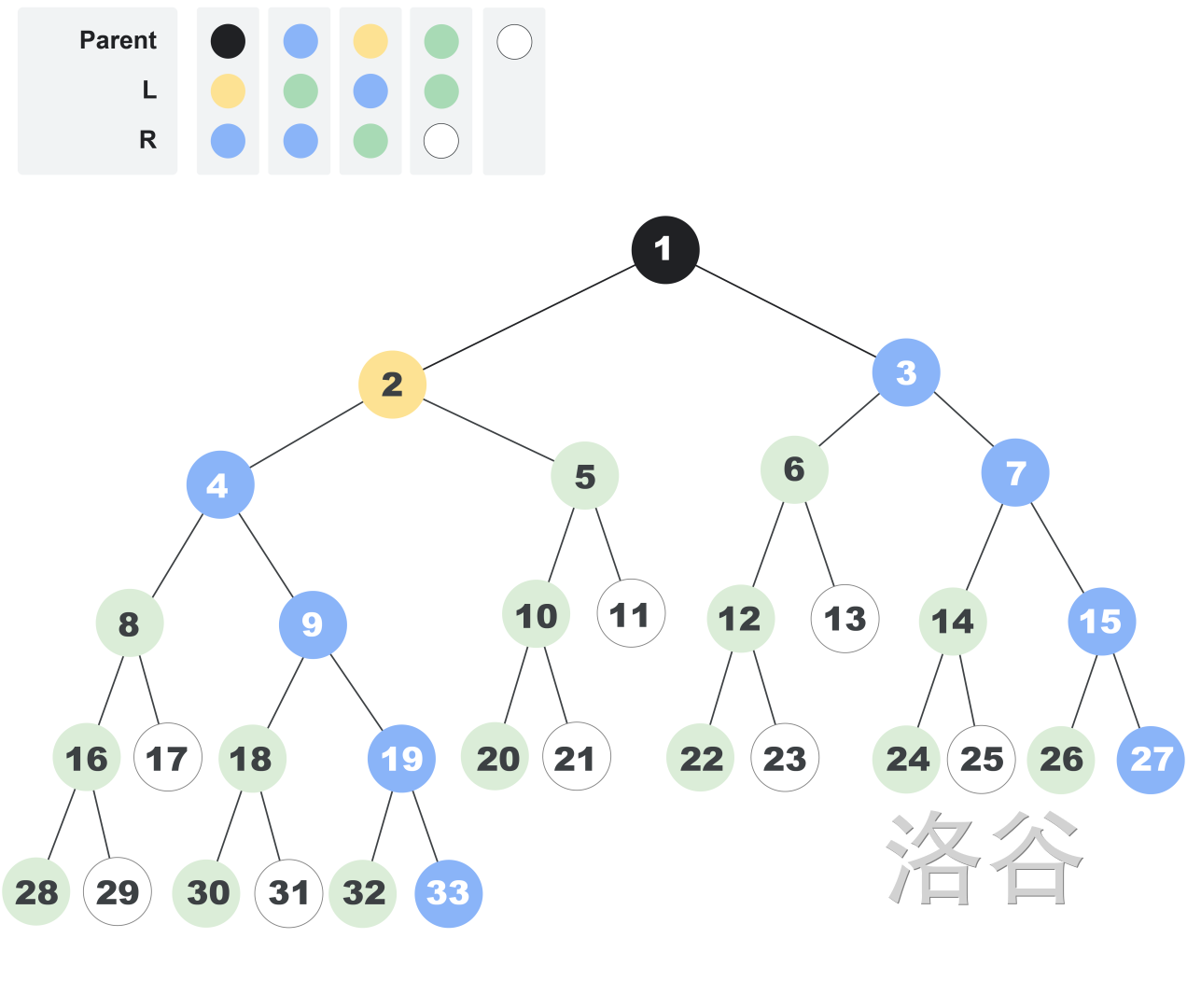
Given the lists $\mathbf{L}$ and $\mathbf{R}$ that define a tree and the indices of two different nodes in the tree, return the distance between those two nodes.

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case consists of three lines. The first line contains $\mathbf{N}$, $\mathbf{A}$, and $\mathbf{B}$: the size of the lists that define the tree, and the indices of the two nodes whose distance you need to calculate, respectively. The second line contains $\mathbf{N}$ integers $\mathbf{L}_{1}$, $\mathbf{L}_{2}$, $\ldots$, $\mathbf{L}_{\mathbf{N}}$ and the third line contains $\mathbf{N}$ integers $\mathbf{R}_{1}$, $\mathbf{R}_{2}$, $\ldots$, $\mathbf{R}_{\mathbf{N}}$, as described above.

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the distance between the nodes with indices $\mathbf{A}$ and $\mathbf{B}$ in the tree defined by the lists $\mathbf{L}$ and $\mathbf{R}$.

5
3 1 8
3 0 0
2 0 2
3 1 5
3 0 0
2 0 2
4 1 27
3 4 2 4
2 2 4 0
4 1 28
3 4 2 4
2 2 4 0
3 1 10
1 3 1
3 2 1

Case #1: 3
Case #2: 2
Case #3: 4
Case #4: 5
Case #5: 3

4
3 5 7
3 0 0
2 0 2
3 4 9
3 0 0
2 0 2
4 11 18
3 4 2 4
2 2 4 0
4 21 22
3 4 2 4
2 2 4 0

Case #1: 4
Case #2: 3
Case #3: 5
Case #4: 8

提示

Sample Explanation

The tree in Sample Cases #1 and #2 is the first tree shown in the statement. The tree in Sample Cases #3 and #4 is the last tree shown in the statement. The same is true for the additional samples below. In Sample Case #5, notice that some colors may not be present in the tree.

Sample Test Set 2 fits the limits of Test Set 2. It will not be run against your submitted solutions.

Limits

• $1 \leq \mathbf{T} \leq 100$.
• $1 \leq \mathbf{N} \leq 50$.
• $0 \leq \mathbf{L}_{i} \leq \mathbf{N}$.
• $0 \leq \mathbf{R}_{i} \leq \mathbf{N}$.
• $\mathbf{A} < \mathbf{B} \leq 10^{18}$.
• The tree defined by $\mathbf{L}$ and $\mathbf{R}$ has at least $\mathbf{B}$ nodes.

Test Set 1 (25 Pts, Visible Verdict)

• $\mathbf{A} = 1$.

Test Set 2 (40 Pts, Hidden Verdict)

• $1 \leq \mathbf{A} \leq 10^{18}$.