题目描述

Gooli is a huge company that owns $\mathbf{B}$ buildings in a hilly area. Five years ago, Gooli built slides that allowed employees to go from one building to another (they are not bidirectional), starting a tradition of building slides between buildings. Currently, $\mathbf{S}$ slides exist.

Melek is Gooli's Head of Transportation and a problem-solving enthusiast. She was tasked with keeping the slides enjoyable to use. The idea she came up with was disabling some slides such that only circuits remained. A circuit is a set of two or more buildings $b_{1}, b_{2}, \ldots, b_{k}$ such that there is exactly one slide enabled from building $b_{i}$ to building $b_{i+1}$, for each $i$, and exactly one slide enabled from building $b_{k}$ to building $b_{1}$. No other slides from or to any of those buildings should be enabled, to prevent misdirection. A state of the slides is then called fun if each building belongs to exactly one circuit.

Slides in Gooli's campus are numbered with integers between 1 and $\mathbf{S}$, inclusive. Melek created a slide controlling console that supports two operations: enable and disable. Both operations receive three parameters $\ell, r$, and $m$ and perform the operation on each slide $x$ such that $\ell \leq x \leq r$ and $x$ is a multiple of $m$. An enable operation is valid only if all affected slides are in a disabled state right before the operation is performed. Similarly, a disable operation is valid only if all affected slides are in an enabled state right before the operation is performed.

The following picture illustrates a possible succession of states and operations. The layout has 3 buildings and 3 slides. Slides are light grey when disabled and dark grey when enabled.

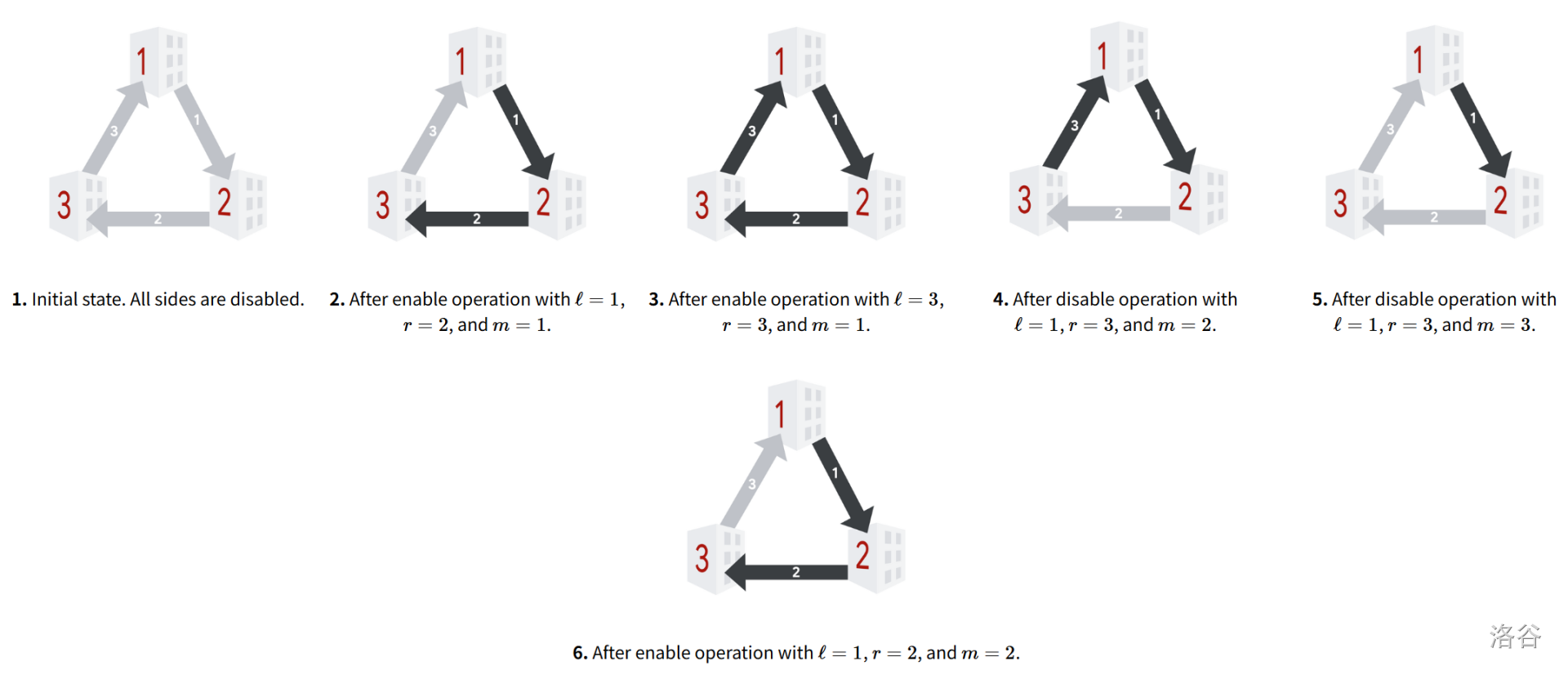
1. Initial state. All sides are disabled.
2. After enable operation with $\ell=1$, $r=2$, and $m=1$.
3. After enable operation with $\ell=3$, $r=3$, and $m=1$.
4. After disable operation with $\ell=1, r=3$, and $m=2$.
5. After disable operation with $\ell=1, r=3$, and $m=3$.
6. After enable operation with $\ell=1, r=2$, and $m=2$.

Unfortunately, Sult, Melek's cat, found the console and started performing several valid enable and disable operations. After every console operation performed by Sult, Melek wants to know if the state of the slides can be made fun by enabling exactly one currently disabled slide. Note that Melek does not actually enable this slide.

In the picture above, we can see that after the first, third, and last operations, Melek could enable the only disabled slide and get to a fun state. After the second operation, there are two issues. One issue is that there are no currently disabled slides, so Melek cannot enable any. Additionally, the state is already fun, so even if there were additional disabled slides, enabling anything would result in a not fun state. After the fourth operation, there are two disabled slides, but enabling either would not yield a fun state.

All slides are initially disabled, then Sult performs its operations one at a time. After each of Sult's operations, determine which disabled slide, if any, Melek can enable to put the slides in a fun state.

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case starts with a line containing three integers $\mathbf{B}$, $\mathbf{S}$, and $\mathbf{N}$: the number of buildings, slides, and operations to process, respectively. Then, $\mathbf{S}$ lines follow. The $i$-th of these lines contains two integers $\mathbf{X}_{i}$ and $\mathbf{Y}_{i}$, indicating that the slide with number $i$ goes from building $\mathbf{X}_{i}$ to building $\mathbf{Y}_{i}$. Finally, $\mathbf{N}$ lines represent the operations. The $j$-th of these lines contains a character $\mathbf{A}_{j}$ and three integers $\mathbf{L}_{j}, \mathbf{R}_{j}$, and $\mathbf{M}_{j}$, describing the $j$-th operation. $\mathbf{A}_{j}$ describes the type of operation using an uppercase $\mathbf{E}$ for enable and an uppercase $\mathbf{D}$ for disable. The operation is to be performed on slides with numbers that are simultaneously a multiple of $\mathbf{M}_{j}$ and between $\mathbf{L}_{j}$ and $\mathbf{R}_{j}$, inclusive.

输出格式

For each test case, output one line containing Case #x: $y_{1}\ y_{2}\ \ldots\ y_{N}$, where $x$ is the test case number (starting from 1) and $y_{j}$ is an uppercase $\mathbf{X}$ if there is no way to turn the state of slides created by the first $j$ console operations into a fun state by enabling exactly one disabled slide. Otherwise, $y_{j}$ should be an integer representing that enabling the $y_{j}$-th slide would turn the state created by the first $j$ console operations into a fun state.

2
3 3 5
1 2
2 3
3 1
E 1 2 1
E 3 3 1
D 1 3 2
D 1 3 3
E 1 2 2
5 8 10
1 5
5 3
4 1
3 2
2 4
2 5
2 1
1 4
E 1 8 2
D 4 8 2
E 3 5 1
E 1 1 3
E 1 1 1
E 5 8 2
D 1 8 3
D 5 8 4
D 4 5 1
E 3 4 1

Case #1: 3 X 2 X 3
Case #2: 3 X 1 1 X X X 3 X 5

提示

Sample Explanation

Sample Case #1 is the one depicted in the problem statement.

The following picture shows the building and slide layout of Sample Case #2.

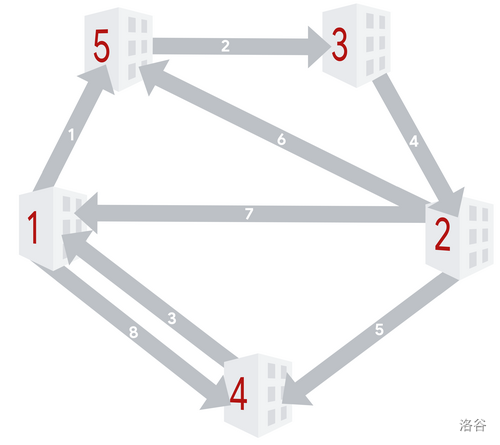
The sets of enabled slides after each operation are:

• $\{2,4,6,8\}$,
• $\{2\}$,
• $\{2,3,4,5\}$,
• $\{2,3,4,5\}$,
• $\{1,2,3,4,5\}$,
• $\{1,2,3,4,5,6,8\}$,
• $\{1,2,4,5,8\}$,
• $\{1,2,4,5\}$,
• $\{1,2\}$, and
• $\{1,2,3,4\}$.

Limits

• $1 \leq \mathbf{X}_{i} \leq \mathbf{B}$, for all $i$.
• $1 \leq \mathbf{Y}_{i} \leq \mathbf{B}$, for all $i$.
• $\mathbf{X}_{i} \neq \mathbf{Y}_{i}$, for all $i$.
• $\left(\mathbf{X}_{i}, \mathbf{Y}_{i}\right) \neq\left(\mathbf{X}_{j}, \mathbf{Y}_{j}\right)$, for all $i \neq j$.
• $\mathbf{A}_{j}$ is either uppercase $\mathbf{E}$ or uppercase $\mathbf{D}$, for all $j$.
• $1 \leq \mathbf{L}_{j} \leq \mathbf{R}_{j} \leq \mathbf{S}$, for all $j$.
• $1 \leq \mathbf{M}_{j} \leq \mathbf{S}$, for all $j$.
• Each operation is valid.

Test Set 1 (10 Pts, Visible Verdict)

• Time limit: 10 seconds.
• $1 \leq \mathbf{T} \leq 100$.
• $2 \leq \mathbf{B} \leq 100$.
• $2 \leq \mathbf{S} \leq 1000$.
• $1 \leq \mathbf{N} \leq 1000$.

Test Set 2 (20 Pts, Hidden Verdict)

• Time limit: 120 seconds.
• $1 \leq \mathbf{T} \leq 30$.
• $2 \leq \mathbf{B} \leq 3 \times 10^{4}$.
• $2 \leq \mathbf{S} \leq 3 \times 10^{5}$.
• $1 \leq \mathbf{N} \leq 3 \times 10^{5}$.