题目描述

Alice and Bob are going to play the Binary Search game. The game is played on a board consisting of a single row of $2^{\mathbf{L}}$ cells. Each cell contains an integer between 1 and $\mathbf{N}$, inclusive. There are also $\mathbf{N}$ cards numbered 1 through $\mathbf{N}$. Before the game starts, the referee writes an integer between 1 and $\mathbf{M}$, inclusive, on each card, in one of the $\mathbf{M}^{\mathbf{N}}$ ways in which that can be done. Alice and Bob know the integers in the cells and on each card before they start playing.

The game proceeds alternating turns, with Alice having the first turn. There are $\mathbf{L}$ turns in total, which means Alice plays $\lceil \mathbf{L}/2 \rceil$ turns and Bob plays $\lfloor \mathbf{L}/2 \rfloor$ turns. During a turn, a player can eliminate either the leftmost half or the rightmost half of the remaining cells. For example, let us consider a board that contains the numbers $[2, 4, 1, 1, 4, 5, 2, 5]$. In her first turn, Alice must choose to eliminate one half, leaving either $[2, 4, 1, 1]$ or $[4, 5, 2, 5]$. If she eliminates the leftmost half and leaves $[4, 5, 2, 5]$, then Bob must choose between leaving $[4, 5]$ and $[2, 5]$. If he were to leave $[2, 5]$, the game's final turn would have Alice choosing between $[2]$ and $[5]$.

When the game is over, they look at the number $X$ in the only remaining cell. The score of the game is the integer written on card number $X$. In the example above, if Alice were to eliminate $[5]$ and leave $[2]$ in her final turn, the score of the game would be the number the referee wrote on card number 2.

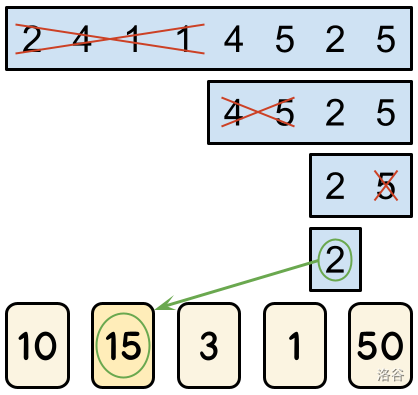
Alice plays optimally to maximize the score of the game, while Bob plays optimally to minimize it. They are given a fixed board with integers $\mathbf{A}_1$, $\mathbf{A}_2$, …, $\mathbf{A}_{2^{\mathbf{L}}}$ in its cells. For maximal fairness, they will play $\mathbf{M}^{\mathbf{N}}$ games, and the referee will choose a different way to write integers on the cards for each one. That means that for any given way of writing integers on the cards, Alice and Bob will play exactly one game with it. Given the game parameters and the fixed board contents, please determine the sum of the scores of all those games. Since the output can be a really big number, we only ask you to output the remainder of dividing the result by the prime $10^9 + 7$ ($1000000007$).

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case consists of exactly two lines. The first line of each test case contains the three integers $\mathbf{N}$, $\mathbf{M}$, and $\mathbf{L}$. The second line contains $2^{\mathbf{L}}$ integers $\mathbf{A}_1$, $\mathbf{A}_2$, …, $\mathbf{A}_{2^{\mathbf{L}}}$, where $\mathbf{A}_i$ is the integer contained in the $i$-th cell from the left of the board.

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the sum of scores of all $\mathbf{M}^{\mathbf{N}}$ games, modulo the prime $10^9 + 7$ ($1000000007$).

3
2 2 2
2 1 1 1
4 3 2
3 1 1 4
5 100 3
2 4 1 1 4 5 2 5

Case #1: 6
Case #2: 144
Case #3: 991661422

提示

Sample Explanation

In Sample Case #1, there are 4 ways to write the integers on the blank cards: $[1, 1], [1, 2], [2, 1]$, and $[2, 2]$. In the first two ways, no matter what Alice chooses in her first turn, Bob can always make the number in the last remaining cell be a 1, and card 1 contains a 1, which means those two games have a score of 1. In the last two ways, Alice can start by eliminating the leftmost half of the board, leaving $[1, 1]$ for Bob, who then has no choice but to leave $[1]$ at the end. Since card 1 has a 2 on it in these ways, the score of both of these games is 2. The sum of all scores is therefore $1 + 1 + 2 + 2 = 6$.

Limits

• $1 \leq \text{T} \leq 12$.
• $1 \leq \text{L} \leq 5$.
• $1 \leq \text{A}_i \leq \text{N}$, for all $i$.

Test Set 1 (9 Pts, Visible Verdict)

• $1 \leq \text{N} \leq 8$.
• $1 \leq \text{M} \leq 100$.

Test Set 2 (26 Pts, Hidden Verdict)

• $1 \leq \text{N} \leq 32$.
• $1 \leq \text{M} \leq 10^9$.