题目描述

You are hired as a temporary employee of the Fence Construction Company and have been tasked with finishing the design of the fencing for a field. Each fence must run in a straight line between two poles. Each pole occupies a single point and the location of each pole is fixed. No three poles are collinear. Fences cannot intersect each other, except possibly at their endpoints (the poles).

The design was started by someone else, but they quit the project after adding exactly two fences. You need to finish their design. To impress your bosses and clients, you want the design to have as many fences as possible, regardless of their lengths.

Given the positions of the poles and the already-built fences, please find a way to add as many fences as possible such that no pair of fences (new or existing) intersect each other, except possibly at their endpoints (the poles).

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case starts with a single line containing an integer $\mathbf{N}$, indicating the number of poles. Then, $\mathbf{N}$ lines follow. The $i$-th of these lines contains two integers $\mathbf{X}_i$ and $\mathbf{Y}_i$, representing the X and Y coordinates of the $i$-th pole's position. The last two lines for each test case represent the two existing fences. These two lines contain two integers each: $\mathbf{P}_k$ and $\mathbf{Q}_k$, representing that the $k$-th existing fence runs between the $\mathbf{P}_k$-th and the $\mathbf{Q}_k$-th pole (poles are numbered starting from 1).

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the maximum number of fences that can be added to the design (not including the existing ones). Then, output $y$ more lines. Each line must contain two distinct integers $i$ and $j$ (both between 1 and $\mathbf{N}$, inclusive), representing a different fence that connects the $i$-th and $j$-th poles. No pair of the $y + 2$ fences (the existing fences as well as the ones you have added) may overlap, except possibly at their endpoints.

2
4
0 0
0 1
1 1
1 0
1 2
3 4
5
0 0
0 1
1 1
1 0
2 3
1 2
3 5

Case #1: 3
1 4
2 3
4 2
Case #2: 6
5 4
2 4
5 2
1 4
4 3
3 2

提示

Sample Explanation

The following pictures show the poles and fences in the given samples. The fences with the wider blue line on them are the existing ones, and the rest show the way of adding a maximum number of fences shown in the sample output.

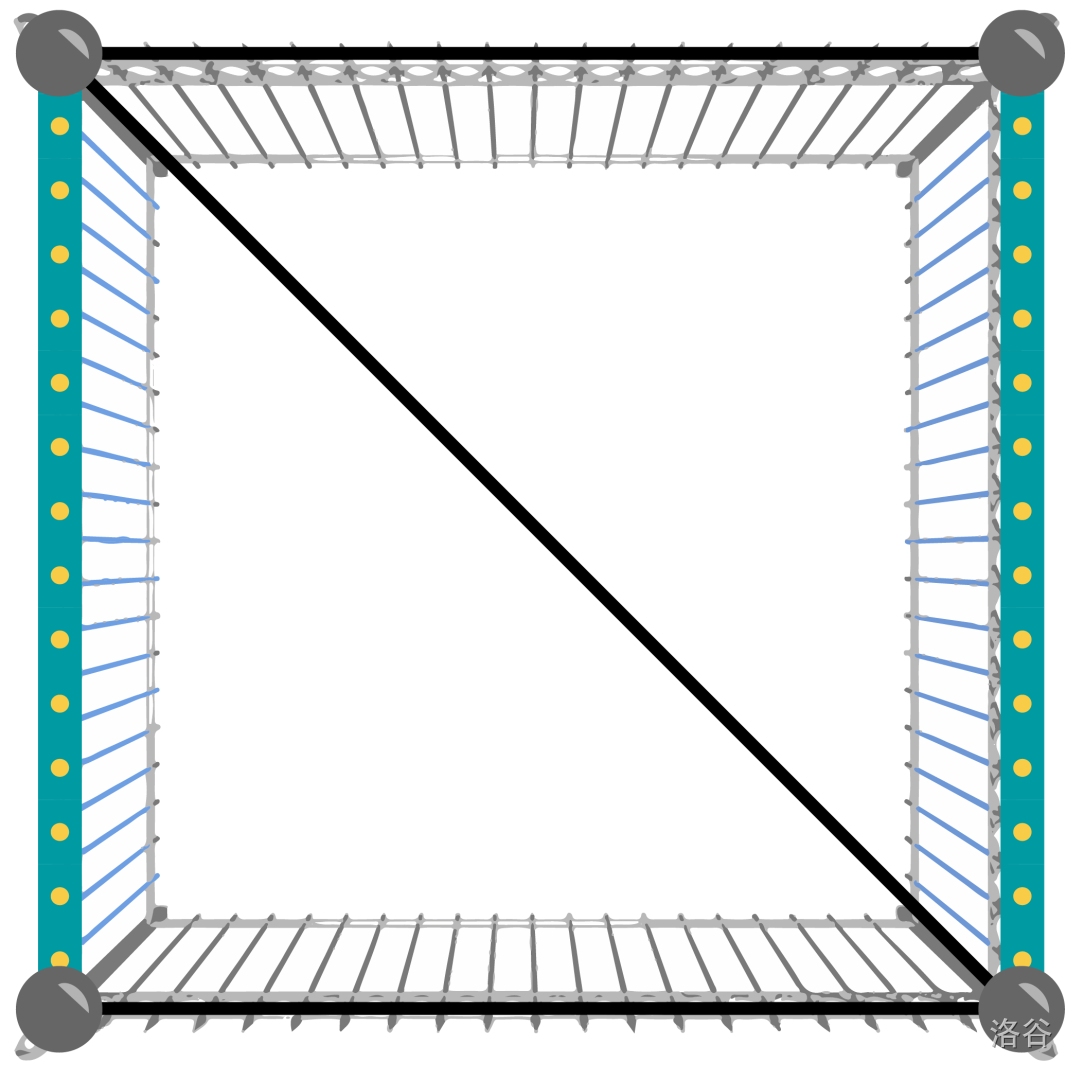
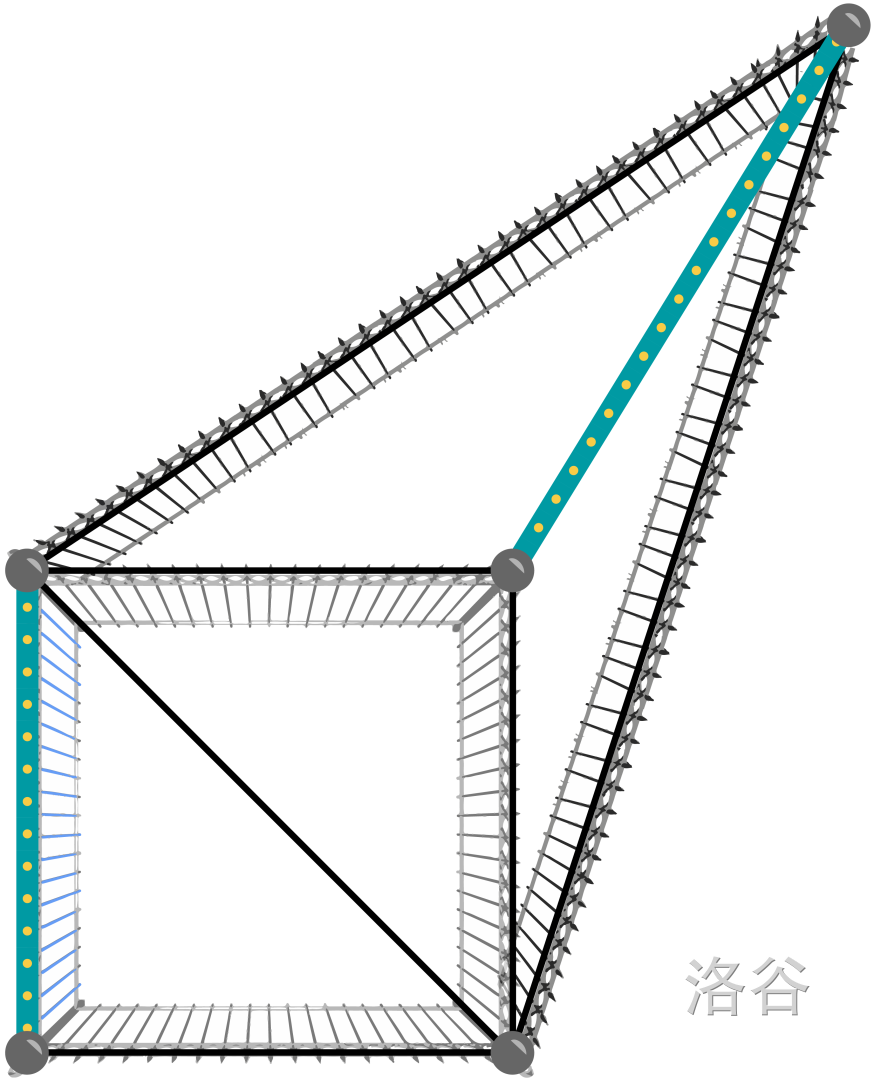
Limits

• $1 \leq \mathbf{T} \leq 50$.
• $-10^9 \leq \mathbf{X}_i \leq 10^9$, for all $i$.
• $-10^9 \leq \mathbf{Y}_i \leq 10^9$, for all $i$.
• $(\mathbf{X}_i, \mathbf{Y}_i) \neq (\mathbf{X}_j, \mathbf{Y}_j)$, for all $i \neq j$.
• $1 \leq \mathbf{P}_k < \mathbf{Q}_k \leq \mathbf{N}$, for all $k$.
• The existing fences do not intersect, except possibly at their endpoints.
• No three poles are collinear.

Test Set 1 (11 Pts, Visible Verdict)

• Time limit: 60 seconds.
• $4 \leq \mathbf{N} \leq 100$.

Test Set 2 (19 Pts, Hidden Verdict)

• Time limit: 90 seconds.
• $4 \leq \mathbf{N} \leq 10^5$.