题目描述

Cody-Jamal's latest artistic installment is a tiled kitchen floor that can be retiled to different patterns. The floor consists of a matrix of $\mathbf{R}$ rows and $\mathbf{C}$ columns of square tiles. Each tile is reversible, one side is magenta and the other one is green.

To retile the kitchen, there are two allowed operations:

• flip a tile, changing its visible color from magenta to green, or vice versa, and
• swap two adjacent tiles (horizontally or vertically, but not diagonally), without flipping either.

Viewing Cody-Jamal's artistic floor is free, but interacting with it is not. Performing a single flip operation costs $\mathbf{F}$ coins, and performing a single swap operation costs $\mathbf{S}$ coins.

You can see the current state of the floor and want to turn it into a particular pattern. What is the minimum amount of coins you need to spend to achieve your goal?

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. The first line of a test case contains 4 integers: $\mathbf{R}$, $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{S}$, the number of rows and columns of the floor, the cost in coins of flipping and the cost in coins of swapping, respectively. Then, $2 \cdot \mathbf{R}$ lines follow. The first $\mathbf{R}$ lines contain $\mathbf{C}$ characters each. The $j$-th character of the $i$-th of these lines represents the current state of the tile in the $i$-th row and $j$-th column. The character is $\mathsf{M}$ if the currently visible side is magenta and $\mathsf{G}$ otherwise. The last $\mathbf{R}$ lines also contain $\mathbf{C}$ characters each. The $j$-th character of the $i$-th of these lines represents the color you want for the tile in the $i$-th row and $j$-th column, using the same character code as for the current state.

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the minimum amount of coins you need to spend to perform operations that allow you to change the tile colors from their current state to your intended one.

2
2 4 1 1
MGMG
MMMG
GMGM
MMMM
3 3 1 1
MGG
GMG
MMM
MMM
MGM
MMG

Case #1: 3
Case #2: 4

1
1 5 1000 1
MGGGG
GGGMM

Case #1: 1003

提示

Sample Explanation

In Sample Case #1, there are 5 tiles that have a different color between the current and the desired states of the floor. Since each operation can change at most 2 tiles, at least 3 operations, costing 3 coins, are needed. One way to do it with exactly 3 coins is:

1. Swap the leftmost two tiles in the top row.
2. Swap the rightmost two tiles in the top row.
3. Flip the bottom right corner tile.

The picture below illustrates the states the floor goes through. The highlighted tile or tiles in each state are the ones being changed by the operation.

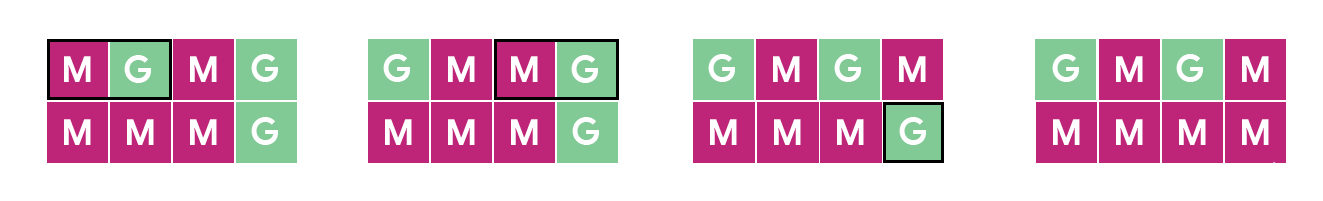
In Sample Case #2, there are 6 tiles that need changing. However, since only swaps can change two tiles at a time, solving it with 3 operations would require all of them to be swaps. There is no way to involve all 6 tiles in a single swap each, so we need at least 4 operations. One way to use exactly 4 operations is:

1. Swap the topmost two tiles in the middle column.
2. Flip the top right corner tile.
3. Swap the bottommost two tiles in the rightmost column.
4. Flip the middle tile of the leftmost column.

The picture below illustrates the states the floor goes through.

Sample Test Set 2 fits the limits of Test Set 2. It will not be run against your submitted solutions.

In the Sample Case for Test Set 2, flips are so expensive that we want to avoid them at all costs. We need at least one since our desired floor state has more magenta tiles than the current one, and swaps do not change that amount. We can do it optimally with just one flip like this:

1. Swap the leftmost two tiles.
2. Flip the rightmost tile.
3. Swap the second and third tiles from the left.
4. Swap the third and fourth tiles from the left.

The picture below illustrates all the states the floor goes through.

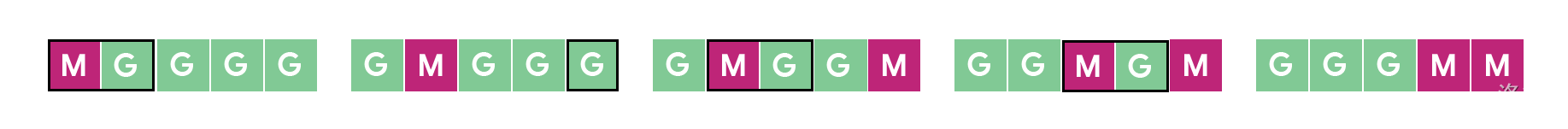
Limits

• $1 \leq \mathbf{T} \leq 100$.
• $1 \leq \mathbf{R} \leq 10$.
• $1 \leq \mathbf{C} \leq 10$.

Test Set 1 (11 Pts, Visible Verdict)

• $\mathbf{F}=1$.
• $\mathbf{S}=1$.

Test Set 2 (23 Pts, Hidden Verdict)

• $1 \leq \mathbf{F} \leq 10^{6}$.
• $1 \leq \mathbf{S} \leq 10^{6}$.