题目描述

You are going to build $N$ towers of $B$ cubic blocks each, one block at a time. Towers are built bottom-up: the $i$-th block to be placed in a tower ends up as the $i$-th from the bottom. You need to decide where to place each block before getting to see any of the upcoming blocks, and once placed, blocks cannot be moved.

Each block has a single decimal digit printed on it, and towers are built such that the faces with digits are all facing the front. The font is such that blocks cannot be rotated to obtain a different digit (for example, a block with a 6 on it cannot be rotated to obtain a block with a 9 on it, nor vice versa).

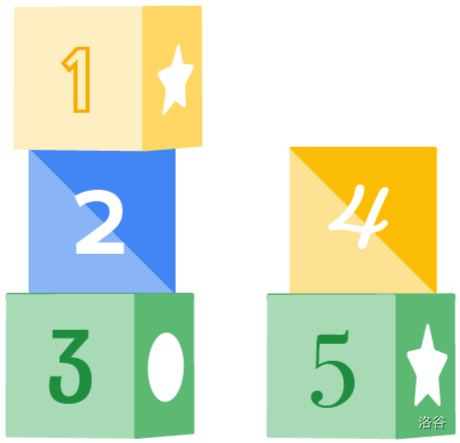
For example, suppose $N = 3$ and $B = 3$ and you currently have towers as shown in Picture 1. If a block with a 6 shows up next, you have two options: either place it on top of the tower with only two blocks (as shown in Picture 2) or start the third tower (as shown in Picture 3). Note that you cannot put it on top of the first tower since the first tower already has $B$ blocks.

After the building is done, we read the $B$ digit integer printed on the front of each tower from the top to the bottom (that is, the digit on the last block placed on a tower is the most significant digit). Notice that these integers may have any number of leading zeroes. Then, we add those $N$ integers together to obtain the score of our building operation.

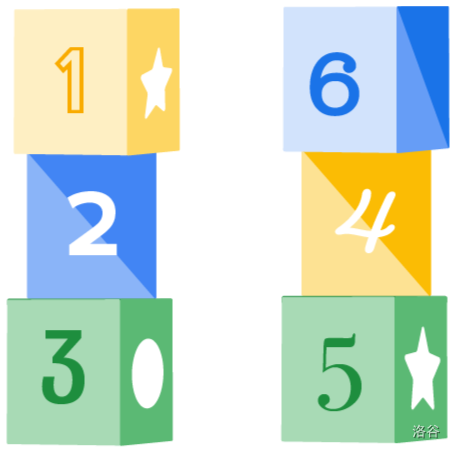
For example, in Picture 4 below, the integers read on each tower, from left to right, are $123$, $345$, and $96$. The score of that building operation would be $123 + 345 + 96 = 564$.

The digit for each block is generated uniformly at random, and independently of any other information. In order for your solution to be judged correct, the sum of its scores over all $\textbf{T}$ test cases must be at least $\textbf{P}$.

Interactive Protocol

This is an interactive problem.

Initially the judge will send you a single line containing four integers $\textbf{T}$, $\textbf{N}$, $\textbf{B}$, and $\textbf{P}$: the number of test cases, the number of towers, the number of blocks in each tower, and the minimum total score you need to reach to pass this test set.

Then, you must process $\textbf{T}$ test cases. Each test case consists of $\textbf{N} \times \textbf{B}$ exchanges. Each exchange corresponds to placing one block. Within each exchange, the judge will first print a line containing a single integer $\textbf{D}$ representing the digit printed on the block you need to place. You need to respond with a single line containing a single integer $\textbf{i}$, the number (between $1$ and $\textbf{N}$) of the tower you want to place that block on.

After the last exchange of each test case except the last one, the judge will immediately start the next test case. After the last exchange of the last test case, the judge will print an additional line containing a single integer: $1$ if your total score is at least $\textbf{P}$ or $-1$ if it is not.

If the judge receives an invalidly formatted line, an invalid tower number, or the number of a tower that already contains $\textbf{B}$ blocks from your program, the judge will print a single number $-1$. After the judge prints $-1$ for any of the reasons explained above, it will not print any further output. If your program continues to wait for the judge after receiving a $-1$, your program will time out, resulting in a Time Limit Exceeded error. Notice that it is your responsibility to have your program exit in time to receive a Wrong Answer judgment instead of a Time Limit Exceeded error. As usual, if the memory limit is exceeded, or your program gets a runtime error, you will receive the appropriate judgment.

You can assume that the digit for each block is generated uniformly at random, and independently for each digit, for each test case and for each submission. Therefore even if you submit exactly the same code twice, the judge could use different random digits.

输入格式

See Interactive Protocol.

输出格式

See Interactive Protocol.

2 3 3 1500
3

2

5

4

1

6

3

9

0

1

1

2

2

1

3

2

3

3

提示

Sample Explanation

In the sample, we are now at the state shown in Picture 4 (sum = 564).

You can use this testing tool to test locally or on our platform. To test locally, you will need to run the tool in parallel with your code; you can use our interactive runner for that.

Instructions for the testing tool are included in comments within the tool. We encourage you to add your own test cases. Please be advised that although the testing tool is intended to simulate the judging system, it is NOT the real judging system and might behave differently.

Limits

• $\textbf{T} = 50$.
• $\textbf{N} = 20$.
• $\textbf{B} = 15$.
• $\textbf{D}$ is a decimal digit between $0$ and $9$.

Test Set 1 (16 Pts, Visible Verdict)

$\textbf{P} = 860939810732536850$ (approximately $8.6 \times 10^{17}$).

Note that this boundary is chosen as approximately $90\%$ of $\textbf{T} \times S$, where $S = 19131995794056374.42\dots$ (approximately $1.9 \times 10^{16}$) is the highest possible expected score that a solution to this problem can achieve on one test case given unbounded running time.

The exact value of $S$ as defined above can be found in lines 13 and 14 of the local testing tool.

Test Set 2 (21 Pts, Visible Verdict)

$\textbf{P} = 937467793908762347$ (approximately $9.37 \times 10^{17}$).

Note that this boundary is chosen as approximately $98\%$ of $\textbf{T} \times S$.