题目背景

待到缘分耗尽，关系断裂，我们还会在一起吗？

题目描述

对于一个排列 $p_{1\sim n}$，建出其大根笛卡尔树，并断开每个点与其右儿子（如果存在）的连边，记最后所成的森林为 $T(p)$。

例如 $p_{1\sim 5} = [1, 3, 2, 5, 4]$，其大根笛卡尔树与 $T(p)$ 分别如下图：

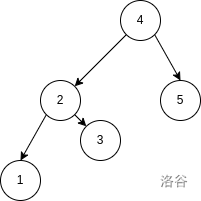
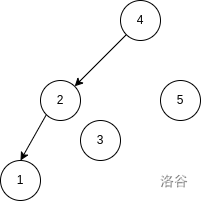
在给定 $n, x, y$ 的情况下，你需要回答，在 $n!$ 种 $1\sim n$ 的排列 $p_{1\sim n}$ 中，有多少种 $p$ 使得节点 $x$ 与节点 $y$ 在 $T(p)$ 中属于同一棵树。节点指的是编号而非在 $p$ 中的权值。

由于答案可能很大，输出的答案需要对一个质数 $P$ 取模。

输入格式

本题有多组测试数据。

第一行，两个正整数 $T, P$，表示测试数据组数与模数。保证 $\bm P$ 为质数。对于每组测试数据：

• 仅一行，三个正整数 $n, x, y$。

输出格式

对于每组测试数据，一行，一个非负整数，表示满足题目条件的排列数量，对 $P$ 取模。

10 1000000007
4 1 4
4 2 2
4 3 2
5 4 2
7 3 5
8 2 7
10 3 8
100 99 6
1000 234 789
5000 1234 4321

6
24
8
25
882
3840
270000
220955222
251832899
768412458

提示

【样例解释】

对于样例的第一组测试数据：有 $[1, 2, 3, 4], [1, 3, 2, 4], [2, 1, 3, 4], [2, 3, 1, 4], [3, 1, 2, 4], [3, 2, 1, 4]$ 共 $6$ 种排列满足条件。

对于样例的第二组测试数据：任意 $1\sim 4$ 的排列均满足条件。

【数据范围】

本题使用捆绑测试。

• 特殊性质 A：$P=998244353$。

对于所有数据：$1\leq T\leq10^6$，$1\le x, y\le n\le 5\times 10^6$，$10^8\le P\le 10^9 + 7$ 且 $P$ 为质数。

【提示】

请使用较快的读入方式。