题目描述

You are given a set $P$ of $\mathbf{N}$ distinct points in the two-dimensional plane. You want to find a maximum set of triangles such that:

• Each vertex of a triangle in your set is a point from $P$ and each point in $P$ is a vertex of at most one triangle in your set.
• Each triangle in your set has positive area (i.e., its 3 vertices are not collinear).
• For any two sides of triangles in your set, their intersection is either empty or an endpoint of one of them.
• For any two triangles in your set, the intersection of the areas strictly inside those triangles is either empty or equal to one of them.

For example, the set of triangles depicted below meets the definition above.

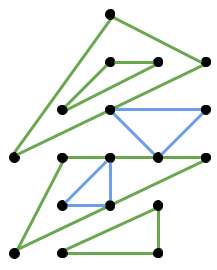
On the other hand, each pair of a yellow and a red triangle in the picture below does not meet the definition.

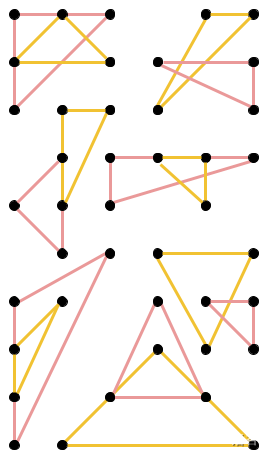
输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case starts with a line containing a single integer $\mathbf{N}$. Then, $\mathbf{N}$ lines follow. The $i$-th of these lines contains two integers $\mathbf{X}_i$ and $\mathbf{Y}_i$ representing the coordinates of the $i$-th point.

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the maximum size of a set of triangles with the desired properties. Then, output $y$ more lines. The $j$-th of those lines must contain $p_j$ $q_j$ $r_j$ representing that the $j$-th triangle in your proposed set has the $p_j$-th, $q_j$-th, and $r_j$-th points in the input as vertices. Points in the input are numbered starting from 1.

3
9
8 2
10 2
2 0
0 5
2 3
10 4
10 0
8 3
2 4
7
0 0
0 3
3 0
0 1
1 0
1 1
2 2
3
0 0
0 1
0 2

Case #1: 3
3 4 5
1 7 9
6 2 8
Case #2: 2
2 3 1
6 5 4
Case #3: 0

提示

Sample Case #1 is illustrated below. Notice that there are other valid ways to construct a maximum number of triangles.

Sample Case #2 is illustrated below. As before, there are other valid ways to construct 2 triangles.

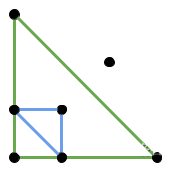
In Sample Case #3, the 3 given points are collinear, so it is not possible to make a valid triangle with them.

Limits

• $1 \leq \mathbf{T} \leq 100$.
• $-10^9 \leq \mathbf{X}_i \leq 10^9$, for all $i$.
• $-10^9 \leq \mathbf{Y}_i \leq 10^9$, for all $i$.
• $(\mathbf{X}_i, \mathbf{Y}_i) \neq (\mathbf{X}_j, \mathbf{Y}_j)$, for all $i \neq j$.

Test Set 1 (8 Pts, Visible Verdict)

• $3 \leq \mathbf{N} \leq 12$.

Test Set 2 (42 Pts, Hidden Verdict)

• $3 \leq \mathbf{N} \leq 3000$.