题目背景

还在写题的 Comentropy 突然收到了挑战，竟然是一道力学题！他感到震惊，一看到数据范围就知道该怎么写了，但是过程冗长，于是找到你帮他精简一下。

注：本题没有严格的物理理论基础，且本题并不要求物理基础。

建议阅读形式化题意。

题目描述

现在有 $n\times n$ 个正方体物块摆成一个方阵，物块有自己的重量，你现在需要控制它们平衡不动。这就要求对于第 $i$ 行第 $j$ 列的物块，它底面受到的支持力在区间 $[l_{i,j},r_{i,j}]$ 中。

出题人们给出横纵方向各 $n$ 根钢丝用以给底面支持力，并把物块放置在钢丝交点处。现在你可以给这 $2n$ 根钢丝分别施加力。（注意同一根钢丝处处的力是相同的）

规定：在数值上，物块受到的支持力就是你施加给其下的两根钢丝的力的和。

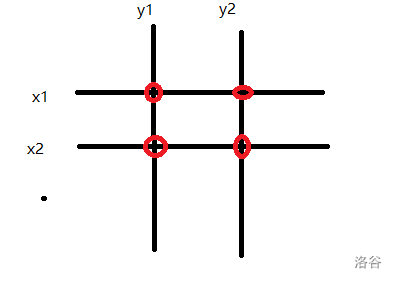
如图，有两组钢丝一组横着放，施加给它们的力分别是：$[x_1,x_2,\dots,x_n]$；一组竖着放，施加给它们的力分别是：$[y_1,y_2,\dots,y_n]$，交点 $(i,j)$ 处的合力即为：$x_i+y_j$。

请你求出每根钢丝的使用力的情况。出题人们为了难倒 Comentropy，还要求序列 $[x_1,x_2,\dots,x_n,y_1,y_2\dots,y_n]$ 的字典序最小。你能帮他处理这个问题吗？

每个力都应当是非负整数，方向向上。

形式化地： 给出两个 $n\times n$ 的矩阵 $l,r$，要求 $l_{i,j}\leq x_i+y_j \leq r_{i,j}$，求一个字典序最小的非负整数解的序列 $\{x\}$, $\{y\}$（把 $x$ 和 $y$ 的序列并起来 $[x_1,x_2,\dots,x_n,y_1,y_2,\dots,y_n]$ 的字典序最小）。

输入格式

第一行，一个正整数 $n(1\leq n \leq 500)$ 表示这是一个 $n \times n$ 的矩阵。

第 $2$ 到 $n+1$ 行，一个矩阵表示受力下界 $l$。

第 $n+2$ 到第 $2n+1$ 行，又一个矩阵表示受力上界 $r$。

输出格式

如果无解，直接输出 -1。

否则：

第一行 $n$ 个数，表示横排钢丝的受力 $x_1,...,x_n$。

第二行 $n$ 个数，表示竖排钢丝的受力 $y_1,...,y_n$。

注意如有多组答案，请输出字典序最小的一组。

2
2 4
1 5
3 5
2 7

0 0 
2 5

提示

样例 1 解释： 可能有另一组解 $x_1=2,x_2=2,y_1=0,y_2=3$，但是 $\{0,0\},\{2,5\}$ 是一组字典序更小的解，且能证明字典序最小。

对于 $10\%$ 的数据，保证 $1\leq n\leq 7,0 \leq r_{i,j}\leq 7$。

对于 $20\%$ 的数据，保证 $1\leq n\leq 50$，$1 \leq l_{i,j}\leq r_{i,j} \leq 200$。

对于 $40\%$ 的数据，保证 $1\leq n\leq 200$。

对于另外 $20\%$ 的数据，保证 $l_{i,j}=r_{i,j}$。

对于 $100\%$ 的数据，保证 $1\leq n\leq 500$，$0 \leq l_{i,j} \leq r_{i,j} \leq 10^9$。

请注意常数给程序带来的运行效率影响。