题目描述

The Coordinate Control Organization has developed an autonomous robot to patrol $N$ distinct important locations on a two-dimensional plane. The $i$-th location has coordinates $(x_i, y_i)$, and it is guaranteed that no three locations lie on a common line.

To help guide the robot, you may paint some line segments on the ground. Each segment must directly connect two important locations, and no two segments may intersect, except possibly at their endpoints.

The robot will begin its patrol at the midpoint of an arbitrary segment, facing towards one of its endpoints. It will move indefinitely according to the following procedure:

• As long as the robot is in the interior of a segment, it will move forward, towards a segment endpoint.
• When the robot reaches an important location, it will initially be facing directly away from the segment it just traversed. The robot will turn right/clockwise until its line of vision is aligned with a segment that leads away from the current location. The robot will then begin moving along this new segment.

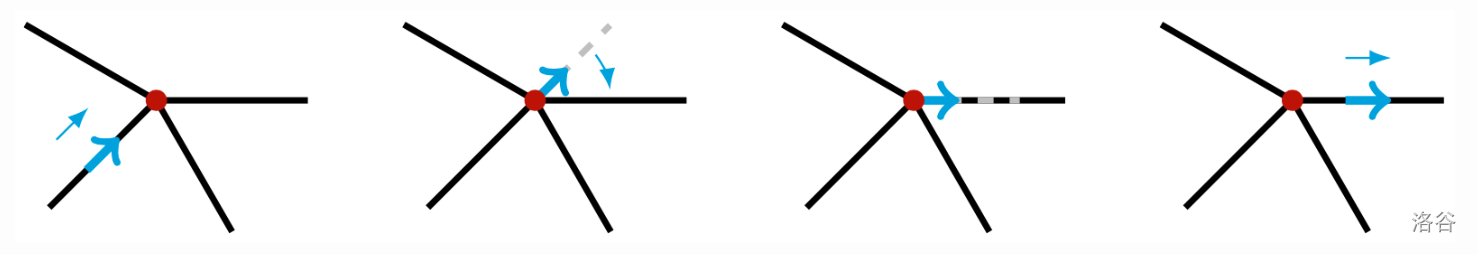
Your task is to paint the segments in such a way that, no matter where the robot starts, it is guaranteed to visit every important location infinitely often. It can be proven that this is always possible.

输入格式

The first line of input contains a single integer $N (2 \leq N \leq 2000)$, the number of important locations.

The next $N$ lines of input each contain two space-separated integers, $x_i$ and $y_i$ ($-10^9 \leq x_i, y_i \leq 10^9$), the coordinates of the $i$-th important location.

It is guaranteed that all $N$ important locations are distinct and no three lie on a common line.

输出格式

On the first line, output a positive integer $M$, the number of line segments you paint on the ground.

The next $M$ lines of output should each contain two space-separated integers, $u_i$ and $v_i$ ($1 \leq u_i, v_i \leq N$, $u_i \neq v_i$), denoting that you paint a line segment between the $u_i$-th and $v_i$-th important locations.

If there are multiple acceptable answers, output any of them.

4
0 0
1 1
1 2
2 1

3
1 2
2 3
2 4

8
0 0
0 3
1 1
1 2
4 1
4 2
5 0
5 3

9
1 2
2 4
4 8
8 7
7 5
5 1
3 4
4 5
5 6

提示

Sample 1 Explanation

The important locations and painted segments are shown in the following figure:

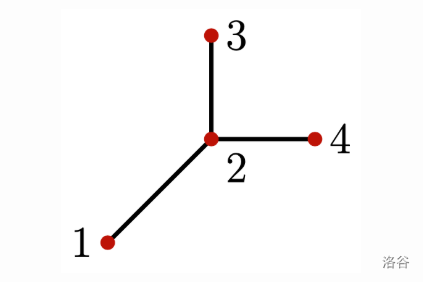
No matter where the robot starts, it will visit every important location infinitely many times. For example, if the robot starts in the middle of the segment between locations $1$ and $2$, facing towards location $2$, the locations the robot will visit in order are:

$$2, 4, 2, 3, 2, 1, 2, 4, \ldots,$$

where the underlined portion is repeated infinitely.

Sample 2 Explanation

The important locations and painted segments are shown in the following figure:

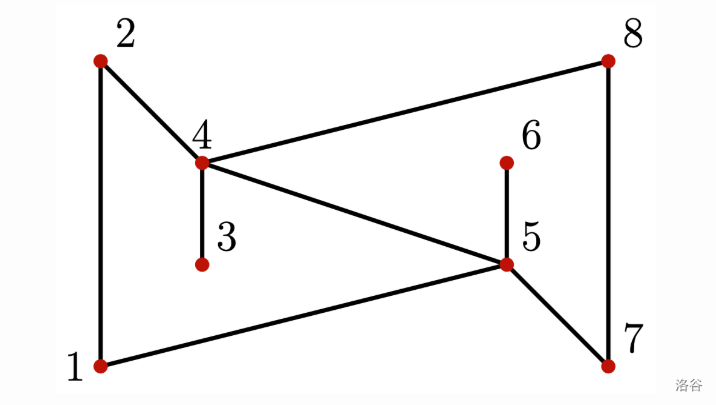
No matter where the robot starts, it will visit every important location infinitely many times. For example, if the robot starts in the middle of the segment between locations $4$ and $5$, facing towards location $5$, the locations the robot will visit in order are:

$$5, 7, 5, 6, 5, 1, 2, 4, 3, 4, 8, 7, 5, \ldots,$$

where the underlined portion is repeated infinitely. Note that it is not necessary for every segment to be traversed infinitely many times; the solution is valid as long as every location is visited infinitely many times.

The following table shows how the available 25 marks are distributed:

Marks Awarded	Additional Constraints
2 marks	$2 \leq N \leq 4$
4 marks	$2 \leq N \leq 8$
3 marks	$3 \leq N$ and the $N$ points are the vertices of a convex polygon in some order.
7 marks	The $N$ points form a convex polygon with $N-1$ vertices plus an additional point inside the polygon.
9 marks	None