题目描述

It has been almost 15 years since Sphinny became the premiere programming contestant by mastering the art of scheduling contests. She has grown alongside Coding Competitions and graduated into a programming contest organizer, and her Programming Club League (PCL) is the most popular sport in her city.

There are $\mathbf{N}$ bus stops in Sphinny's city, and $\mathbf{M}$ express bus routes. Each route bidirectionally connects two different bus stops, called their endpoints. Because of the popularity of PCL, the driver of each bus routes cheers for exactly one club.

Sphinny has to pick up the contest materials for the $j$-th contest at bus stop $\mathbf{P}_j$ and then the contest will be run in bus stop $\mathbf{C}_j$. She can only use the given bus routes to travel between them. Formally, a path for Sphinny to go from $\mathbf{P}_j$ to $\mathbf{C}_j$ is a list of bus routes such that each two consecutive routes have a common endpoint. Also the first route in the path has $\mathbf{P}_j$ as an endpoint and the last one has $\mathbf{C}_j$ as an endpoint. Notice that the same bus route can be used multiple times in a path. If Sphinny's path from $\mathbf{P}_j$ to $\mathbf{C}_j$ contains one or more bus routes whose driver cheers for club $c$, then club $c$ will join the contest. Otherwise, club $c$ will not join the contest. For organizational reasons, Sphinny needs the number of clubs in each contest to be an odd number.

Given the layout of Sphinny's city's bus routes and the contests' details, find out for how many contests there exists a path for Sphinny to take that can ensure an odd number of clubs joining it.

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow.

The first line of each test case contains three integers $\mathbf{N}$, $\mathbf{M}$, and $\mathbf{Q}$: the number of bus stops, bus routes, and contests, respectively.

Then, $\mathbf{M}$ lines follow representing a different bus route each. The $i$-th of these lines contains three integers $\mathbf{U}_i$, $\mathbf{V}_i$, and $\mathbf{K}_i$, meaning that the $i$-th bus route connects bus stops $\mathbf{U}_i$ and $\mathbf{V}_i$ and its driver cheers for club $\mathbf{K}_i$.

Finally, the last $\mathbf{Q}$ lines represent a contest each. The $j$-th of these lines contains two integers $\mathbf{P}_j$ and $\mathbf{C}_j$, representing that materials for the $j$-th contest need to be picked up at bus stop $\mathbf{P}_j$ and the contest needs to be run at bus stop $\mathbf{C}_j$.

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the number of contests for which Sphinny can find a path that ensures an odd number of clubs join it.

2
5 5 3
1 2 1
2 3 2
2 4 1
2 5 1
4 5 1
1 3
3 4
5 1
3 1 2
1 3 1
1 2
1 3

Case #1: 1
Case #2: 1

1
4 5 2
1 2 3
1 3 3
3 4 7
2 3 3
2 4 6
1 2
1 4

Case #1: 2

提示

Sample Explanation

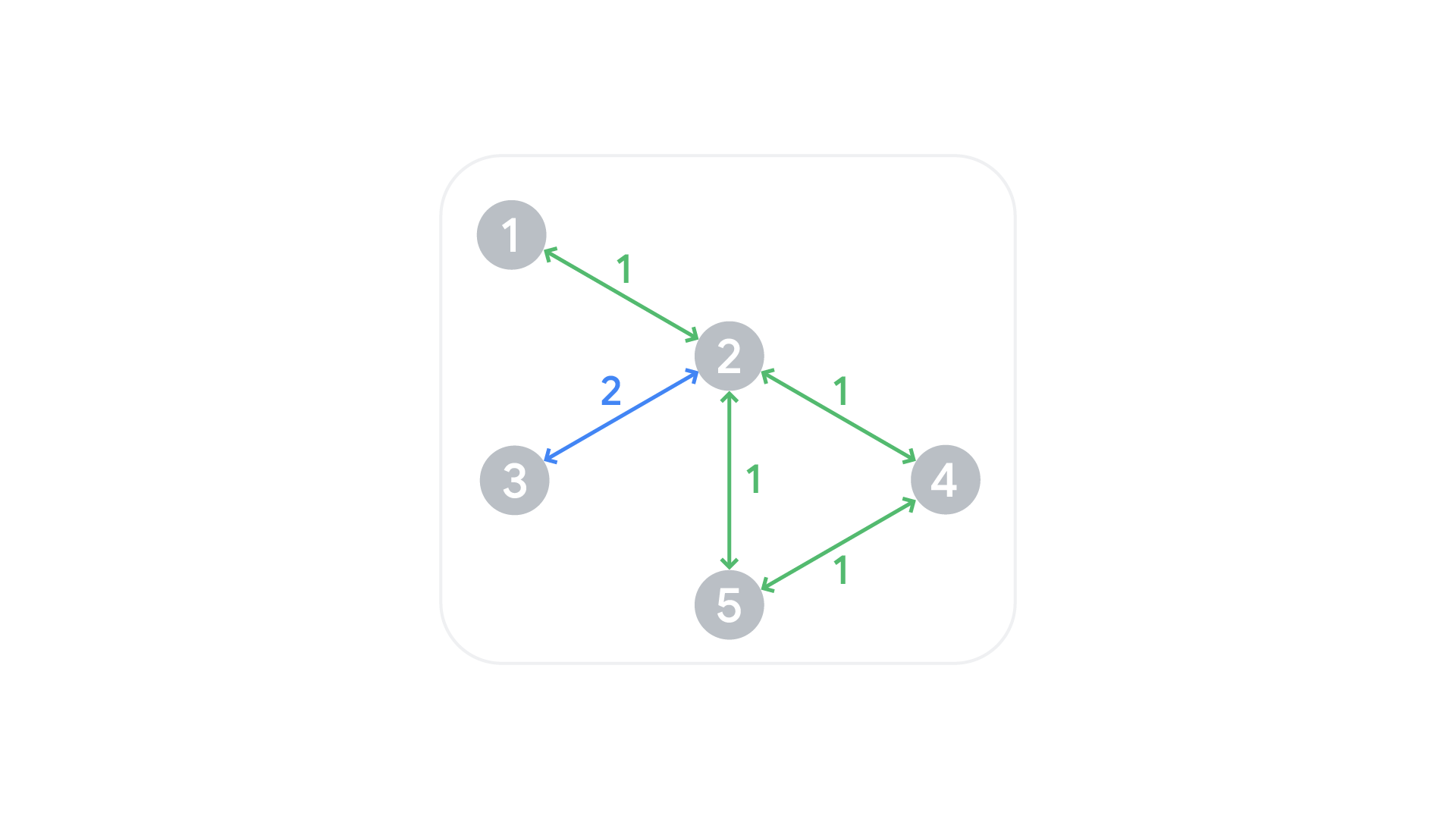
Sample Case #1 is pictured above. In the first two contests, both clubs (green and blue) must be involved in it no matter what path is chosen. For the last contest, it is possible to involve only the green club by using the path through bus stops $1, 2, 4, 5$.

For Sample Case #2, the first contest is not possible because there is no path to go from bus stop $1$ to bus stop $2$. For the second contest, there is a path including the only bus route going bus stop $1$ to bus stop $3$, therefore yielding a contest involving exactly $1$ club, which is an acceptable odd number of clubs.

The following additional sample fits the limits of Test Set 2. It will not be run against your submitted solutions.

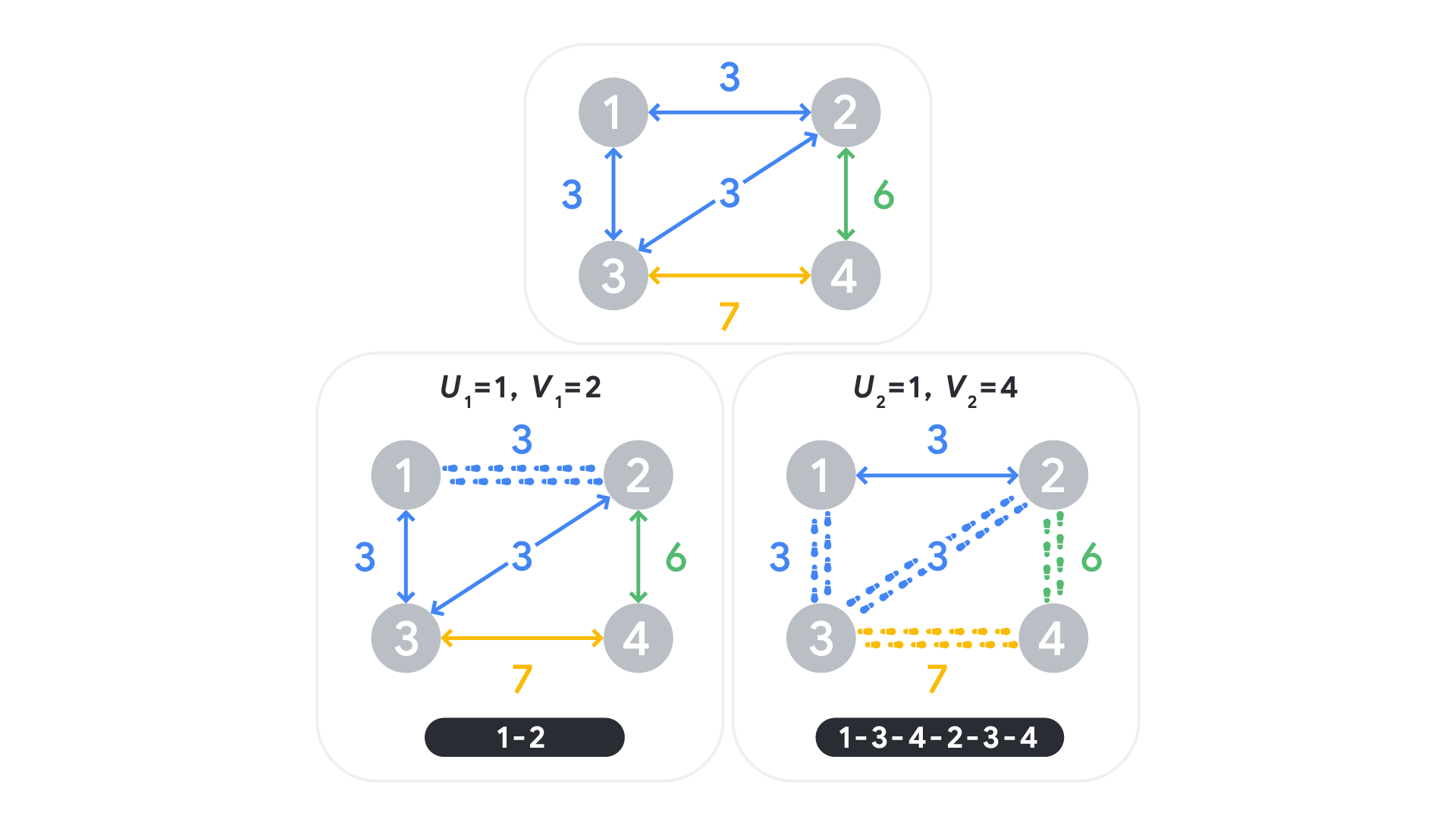
This additional Sample Case is pictured above. In this case, both contests can be done with an odd number of clubs. An example path that achieves that is shown in the picture.

Limits

• $1 \leq \mathbf{T} \leq 100$.
• $1 \leq \mathbf{U}_i \leq \mathbf{N}$, for all $i$.
• $1 \leq \mathbf{V}_i \leq \mathbf{N}$, for all $i$.
• $\mathbf{U}_i \neq \mathbf{V}_i$, for all $i$
• $(\mathbf{U}_i, \mathbf{V}_i) \neq (\mathbf{U}_j, \mathbf{V}_j)$ and $(\mathbf{U}_i, \mathbf{V}_i) \neq (\mathbf{V}_j, \mathbf{U}_j)$, for all $i \neq j$. (No two bus routes have the same pair of endpoints.)
• $1 \leq \mathbf{P}_j \leq \mathbf{N}$, for all $j$.
• $1 \leq \mathbf{C}_j \leq \mathbf{N}$, for all $j$.
• $\mathbf{P}_j \neq \mathbf{C}_j$, for all $j$.

Test Set 1 (7 Pts, Visible Verdict)

• Time limit: 20 seconds.
• $2 \leq \mathbf{N} \leq 500$.
• $1 \leq \mathbf{M} \leq 500$.
• $1 \leq \mathbf{Q} \leq 500$.
• $1 \leq \mathbf{K}_j \leq 2$, for all $j$.

Test Set 2 (6 Pts, Visible Verdict)

• Time limit: 40 seconds.
• $2 \leq \mathbf{N} \leq 500$.
• $1 \leq \mathbf{M} \leq 500$.
• $1 \leq \mathbf{Q} \leq 500$.
• $1 \leq \mathbf{K}_j \leq 100$, for all $j$.

Test Set 3 (10 Pts, Hidden Verdict)

• Time limit: 120 seconds.
• $2 \leq \mathbf{N} \leq 10000$.
• $1 \leq \mathbf{M} \leq 10000$.
• $1 \leq \mathbf{Q} \leq 10000$.
• $1 \leq \mathbf{K}_j \leq 100$, for all $j$.