题目描述

Ada is working on a science project for school. She is studying evolution and she would like to compare how different species of organisms would perform when trying to solve a coding competition problem.

The $\mathbf{N}$ species are numbered with integers between 1 and $\mathbf{N}$, inclusive. Species 1 has no direct ancestor, and all other species have exactly one direct ancestor each, from which they directly evolved. A (not necessarily direct) ancestor of species $x$ is any other species $y$ such that $y$ can be reached from $x$ by moving one or more times to a species direct ancestor starting from $x$. In this way, species 1 is a (direct or indirect) ancestor of every other species.

Through complex genetic simulations, she calculated the average score each of the $\mathbf{N}$ species would get in a particular coding competition. $\mathbf{S}_i$ is that average score for species $i$.

Ada is looking for interesting triplets to showcase in her presentation. An interesting triplet is defined as an ordered triplet of distinct species $(a, b, c)$ such that:

1. Species $b$ is a (direct or indirect) ancestor of species $a$.
2. Species $b$ is not a (direct or indirect) ancestor of species $c$.
3. Species $b$ has an average score strictly more than $\mathbf{K}$ times higher than both of those of $a$ and $c$. That is, $\mathbf{S}_b \geq \mathbf{K} \times \max(\mathbf{S}_a, \mathbf{S}_c) + 1$.

Given the species scores and ancestry relationships, help Ada by writing a program to count the total number of interesting triplets.

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow.

The first line of each test case contains two integers $\mathbf{N}$ and $\mathbf{K}$, denoting the number of species and the factor which determines interesting triplets, respectively.

The second line of each test case contains $\mathbf{N}$ integers $\mathbf{S}_1, \mathbf{S}_2, \ldots, \mathbf{S}_\mathbf{N}$, where $\mathbf{S}_i$ denotes the average score of species $i$.

The third line of each test case contains $\mathbf{N} - 1$ integers $\mathbf{P}_2, \mathbf{P}_3, \ldots, \mathbf{P}_\mathbf{N}$, meaning species $\mathbf{P}_i$ is the direct ancestor of species $i$.

输出格式

For each test case, output one line containing case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the total number of interesting triplets according to Ada's definition.

2
5 2
3 3 6 2 2
3 1 1 3
7 3
2 4 7 2 2 1 8
6 1 7 3 1 3

Case #1: 1
Case #2: 7

提示

Sample Explanation

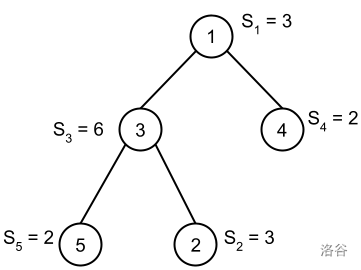
In Sample Case #1, there is only one possible interesting triplet: $(5, 3, 4)$. Indeed, we can verify that:

1. Species $b = 3$ is an ancestor of species $a = 5$.
2. Species $b = 3$ is not an ancestor of species $c = 4$.
3. The score of species $b = 3$ is more than $\mathbf{K}$ times higher than the scores of both $a = 5$ and $c = 4$: $6 = \mathbf{S}_3 \geq \mathbf{K} \times \max(\mathbf{S}_4, \mathbf{S}_5) + 1 = 2 \times \max(2, 2) + 1 = 5$.

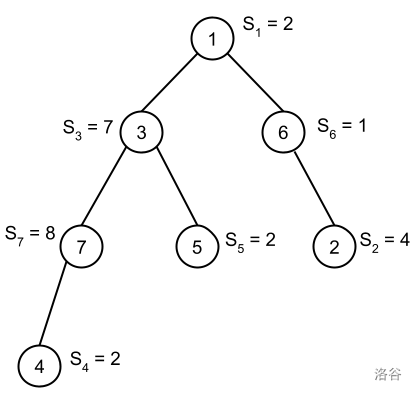
In Sample Case #2, there are seven interesting triplets:

• $(4, 3, 1)$
• $(4, 3, 6)$
• $(4, 7, 1)$
• $(4, 7, 5)$
• $(4, 7, 6)$
• $(5, 3, 1)$
• $(5, 3, 6)$

Limits

• $1 \leq \mathbf{T} \leq 100$.
• $1 \leq \mathbf{K} \leq 10^9$.
• $1 \leq \mathbf{S}_i \leq 10^9$, for all $i$.
• $1 \leq \mathbf{P}_i \leq \mathbf{N}$, for all $i$.
• Species 1 is a (direct or indirect) ancestor of all other species.

Test Set 1 (7 Pts, Visible Verdict)

• $3 \leq \mathbf{N} \leq 1000$.

Test Set 2 (16 Pts, Hidden Verdict)

For at most 30 cases:

• $3 \leq \mathbf{N} \leq 2 \times 10^5$.

For the remaining cases:

• $3 \leq \mathbf{N} \leq 1000$.