题目描述

You are in charge of the management of a railroad network. The network consists of $\mathbf{N}$ stations. Each station $i$ needs to ship goods to exactly one other station $\mathbf{D}_i$. Station $i$ will send exactly one shipment, in a train with exactly $\mathbf{C}_i$ railroad cars.

You get all the shipment information well in advance, so you plan on saving on railroad cars by reusing them. If station $i$ sends $n$ railroad cars to station $\mathbf{D}_i$, then $\mathbf{D}_i$ can add those railroad cars to its supply to use for its own shipment if it did not already happen.

Formally, you must give an initial supply of railroad cars to each station (some stations may get 0) and provide an order for the shipments so that, by the time station $i$ must ship, the number of railroad cars between its initial supply and any previous shipments that arrived at $i$ must be at least the number it needs for its own shipment $\mathbf{C}_i$. You cannot send more than $\mathbf{C}_i$ cars in a shipment out of station $i$, even if the station has more than $\mathbf{C}_i$ available.

For example, suppose that station 1 sends a train carrying exactly 3 railroad cars to station 4. Now, if station 4 needs 2 cars, it could reuse 2 of the cars it received from station 1. And if station 4 needs to send 5 cars, it can reuse all 3 cars received from station 1 and add 2 of its own supply. Note that when station 4 needs to send 2 cars, it cannot send all 3 it received from station 1.

Given the shipment information, what is the minimum number of railroad cars you need to distribute for the stations' initial supplies, such that you can do all shipments in some order?

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case consists of 3 lines. The first line contains a single integer $\mathbf{N}$, the number of stations in the network. The second line contains $\mathbf{N}$ integers $\mathbf{D}_1, \mathbf{D}_2, \ldots, \mathbf{D}_\mathbf{N}$ and the third and last line contains $\mathbf{N}$ integers $\mathbf{C}_1, \mathbf{C}_2, \ldots, \mathbf{C}_\mathbf{N}$. These represent that station $i$ must send a train of exactly $\mathbf{C}_i$ railroad cars to station $\mathbf{D}_i$.

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the minimum number of railroad cars you need to distribute among the stations so that all shipments can be performed.

3
4
2 3 4 3
4 3 2 1
4
2 3 4 1
1 3 1 3
7
3 5 2 5 3 7 6
3 4 6 3 5 1 2

Case #1: 4
Case #2: 5
Case #3: 10

提示

Sample Explanation

In Sample Case #1 one optimal way is to do the shipments in increasing order of departure station. That requires sending 4 cars to station 1. But after that, each station receives enough cars for its shipment, for a total of 4 overall. Since no cars arrive at station 1, it definitely needs the initial 4, so this is also the minimum possible.

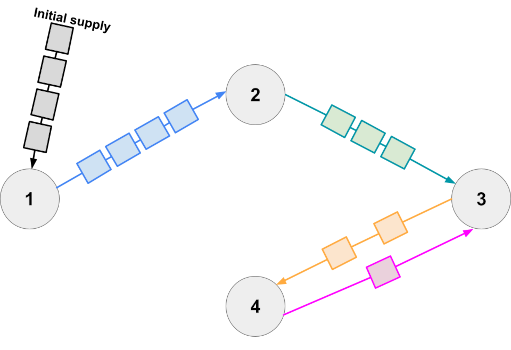
In Sample Case #2 one minimal way is to supply 1 car to station 3 and 2 cars each to stations and 2 and 4, for a total of 5. Then, we can start with the shipment $3 \rightarrow 4$ which gets one additional car to station 4. This makes station 4 have the 3 cars it needs to ship $4 \rightarrow 1$. Station 1 now has 3 cars which is enough to do $1 \rightarrow 2$ with a single car, taking the total at station 2 to 3 cars, enough to do the final shipment $2 \rightarrow 3$. Notice that the shipment $1 \rightarrow 2$ cannot bring extra cars to station 2, even though there are cars available and it would be helpful to do so. There are other ways to do all shipments with 5 initial cars, but no way to do it with less.

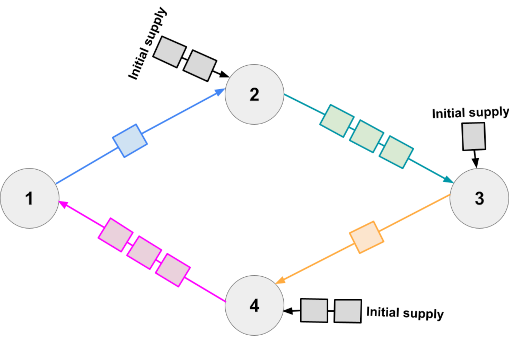
In Sample Case #3, one optimal starting number of cars is 3 cars at stations 1 and 4 and 2 cars at stations 5 and 7.

Limits

• $1 \leq \mathbf{T} \leq 100$.
• $1 \leq \mathbf{D}_{\mathbf{i}} \leq \mathbf{N}$, for all $i$.
• $\mathbf{D}_{\mathbf{i}} \neq i$, for all $i$.
• $1 \leq \mathbf{C}_{\mathbf{i}} \leq 10^{9}$, for all $i$.

Test Set 1 (9 Pts, Visible Verdict)

• $2 \leq \mathbf{N} \leq 8$.

Test Set 2 (20 Pts, Visible Verdict)

• $2 \leq \mathbf{N} \leq 10^{5}$.