题目描述

Onyaomale is leading a project to exchange the lightbulbs from street lights along a freeway from incandescent ones to LED lightbulbs that are both more energy-efficient and powerful. She started by taking all the old incandescent lightbulbs out, and is now focused on installing the new LED ones. Because the new lightbulbs are more powerful, Onyaomale thinks it is possible that some street lights are not necessary and she can save even more energy by not using them.

We model the freeway as a straight line measuring $\mathbf{M}$ meters that goes from west to east. The $x$-th meter is a point that is $x$ meters to the east of the western end of the freeway. If a street light is located at the $x$-th meter, and a lightbulb with an illumination radius of $\mathbf{R}$ meters is installed on it, then the street light illuminates the segment of freeway starting at the $\max(0, x - \mathbf{R})$-th meter and ending at the $\min(\mathbf{M}, x + \mathbf{R})$-th meter, inclusive. Onyaomale needs to install lightbulbs in such a way that every point of the freeway is illuminated by at least one of them. Notice that this includes illuminating points that are not an integer number of meters away from the freeway endpoints. Street lights that are left without a lightbulb do not illuminate anything.

Given the length of the freeway in meters $\mathbf{M}$, the illumination radius of the new lightbulbs $\mathbf{R}$ and the locations of all street lights, find the minimum number of lightbulbs Onyaomale needs to install to illuminate the whole freeway, or report that it is impossible to do so.

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case consists of two lines. The first line contains three integers $\mathbf{M}$, $\mathbf{R}$, and $\mathbf{N}$: the length, in meters, of the freeway, the illumination radius, in meters, of the lightbulbs and the number of street lights, respectively. The second line of a test case contains $\mathbf{N}$ sorted integers $\mathbf{X}_1$, $\mathbf{X}_2$, $\ldots$, $\mathbf{X}_\mathbf{N}$ representing the meters of the freeway where street lights are located.

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the minimum number of lightbulbs Onyaomale needs to install to illuminate the whole freeway, if it is possible. If there is no way to illuminate the entire freeway using the current street lights, $y$ should be IMPOSSIBLE instead.

3
10 3 3
2 7 9
10 2 3
2 7 9
10 2 4
2 3 7 9

Case #1: 2
Case #2: IMPOSSIBLE
Case #3: 4

提示

Sample Explanation

In Sample Case #1, Onyaomale can illuminate the entire freeway by placing bulbs in the western-most and middle street lights only, leaving the eastern-most one unused. With these two lights covering $[0,5]$ and $[4,10]$, the entire freeway $([0,10])$ is illuminated.

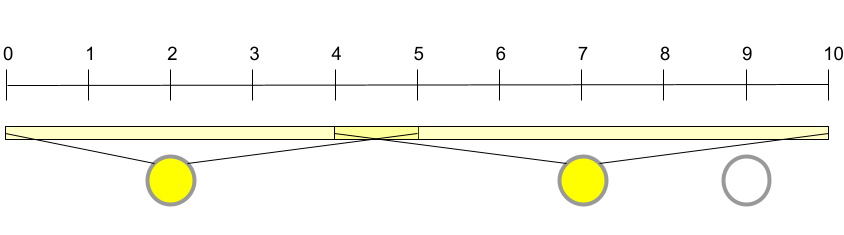
In Sample Case #2, Onyaomale has the same configuration as in Sample Case #1, but with weaker lightbulbs. In this case, there is no way for her to illuminate the entire freeway. In particular, even if all the street lights are lit, the middle point between the $4$-th and $5$-th meters would still not be illuminated.

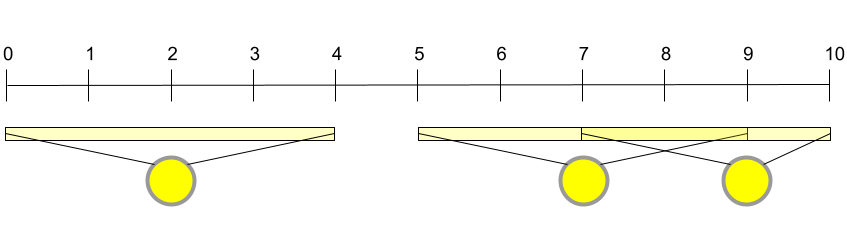
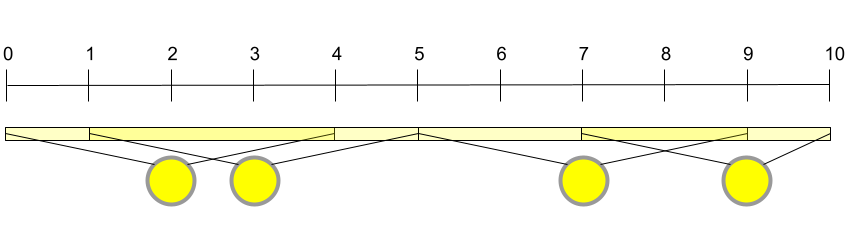
For Sample Case #3 Onyaomale has an additional street light at the $3$-th meter, compared to Sample Case #2, while all other conditions are the same. In this case, installing a lightbulb in every street light is the only way to have the entire freeway illuminated.

Limits

• $1 \leq \mathbf{T} \leq 100.$
• $1 \leq \mathbf{M} \leq 10^{9}.$
• $1 \leq \mathbf{R} \leq 10^{9}.$
• $0 \leq \mathbf{X}_{1}.$
• $\mathbf{X}_{i} < \mathbf{X}_{i+1}, \text{ for all } i.$
• $\mathbf{X}_{\mathbf{N}} \leq \mathbf{M}.$

Test Set 1 (4Pts, Visible Verdict)

• $1 \leq \mathbf{N} \leq 10.$

Test Set 2 (10Pts, Visible Verdict)

• $1 \leq \mathbf{N} \leq 10^{5}.$