题目描述

NE(E)RC featured a number of problems in previous years about cactuses --- connected undirected graphs in which every edge belongs to at most one simple cycle. Intuitively, a $\textit{cactus}$ is a generalization of a tree where some cycles are allowed. The traditional cactus that was initially used in NEERC 2005 problem is given on the second picture in the Examples section.

You are given $n$ integers $d_1, d_2, \ldots, d_n$. Construct any cactus with $n$ vertices such that vertex $i$ has degree $d_i$ (i.e. exactly $d_i$ incident edges), or determine that no such cactus exists. Parallel edges and loops are not allowed.

输入格式

The first line contains a single integer $n$ ($2 \le n \le 2\,000$) --- the number of vertices in the cactus.

The second line contains $n$ integers $d_1, d_2, \ldots, d_n$ ($1 \le d_i \le n-1$) --- the desired vertex degrees.

输出格式

If it's impossible to construct a cactus satisfying the conditions, output a single integer $-1$.

Otherwise, by tradition, output the constructed cactus as a set of edge-distinct paths.

In the first line output an integer $m$ --- the number of such paths. Each of the following $m$ lines should contain a path in the graph. A path should start with an integer $k_i$ ($k_i \ge 2$) followed by $k_i$ integers from $1$ to $n$. These $k_i$ integers should represent consecutive vertices of this path. Adjacent vertices in the path should be distinct. The path can visit the same vertex multiple times, but every edge of the cactus should be traversed exactly once in the whole output.

5
2 2 3 2 1

4
2 1 2
2 2 3
2 3 1
3 3 4 5

4
3 3 2 2

-1

6
1 2 1 1 2 1

-1

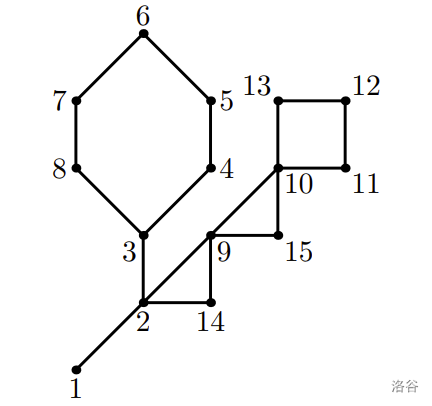
15
1 4 3 2 2 2 2 2 4 4 2 2 2 2 2

3
9 1 2 3 4 5 6 7 8 3
7 2 9 10 11 12 13 10
5 2 14 9 15 10

提示

Sample 1

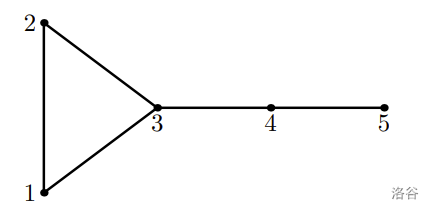
Sample 4

Both in the second and the third example, there exist graphs that satisfy the given conditions but none of them are cactuses.