题目背景

翻译来自于 LibreOJ。

题目描述

题目译自 XXX Olimpiada Informatyczna – II etap Gra w kolorowanie

涂色游戏的棋盘由 $n$ 个格子组成，编号从 $1$ 到 $n$，部分格子相邻，恰有 $n-1$ 对相邻格子，且任意两格子可通过相邻格子连通（棋盘构成一棵树）。

游戏由两名玩家参与。初始时，所有格子为白色，除一个格子涂为红色（属于玩家一）和另一个格子涂为蓝色（属于玩家二）。玩家轮流行动，每次选择一个自身颜色的格子 $u$，并将其相邻的任一白色格子 $v$ 涂为同色。无法行动的玩家输掉游戏。

我们想知道，玩家一在哪些初始格子选择下能确保获胜，即无论玩家二如何行动，玩家一总有制胜策略。具体而言，给定格子集合 $A$ 和 $B$，计算满足以下条件的不同格子对 $(a, b)$ 数量：初始红色格子 $a \in A$，初始蓝色格子 $b \in B$，且玩家一有制胜策略。

程序需处理集合 $A$ 和 $B$ 的 $q$ 次更新，每次添加或移除一个格子，输出每次更新后满足条件的 $(a, b)$ 对数量。

输入格式

第一行包含一个整数 $n$ $(1 \leq n \leq 500000)$，表示棋盘格子数。

接下来的 $n-1$ 行，每行包含两个整数 $u, v$ $(1 \leq u, v \leq n)$，表示格子 $u$ 和 $v$ 相邻。

下一行包含三个整数 $S_A, S_B, q$ $(1 \leq S_A, S_B \leq n, 0 \leq q \leq 500000)$，分别表示集合 $A$ 和 $B$ 的初始大小及更新次数。

下一行包含 $S_A$ 个互不相同的整数（属于 $\{1, \ldots, n\}$），表示集合 $A$ 的格子编号。

下一行包含 $S_B$ 个互不相同的整数（属于 $\{1, \ldots, n\}$），表示集合 $B$ 的格子编号。

接下来的 $q$ 行，每行包含两个字符 $z, t$ 和一个整数 $w$ $(z \in \{\texttt{A}, \texttt{B}\}, t \in \{\texttt{+}, \texttt{-}\}, 1 \leq w \leq n)$，分别表示操作的集合（$A$ 或 $B$）、操作类型（$\texttt{+}$ 为添加，$\texttt{-}$ 为移除）和格子编号 $w$。保证每次操作有效（添加时 $w$ 不在集合，移除时 $w$ 在集合）。

集合 $A$ 和 $B$ 可不互斥，计数的 $(a, b)$ 对要求 $a \neq b$。

输出格式

输出 $q+1$ 行，第 $i$ 行包含一个整数，表示前 $i-1$ 次更新后，满足条件的 $(a, b)$ 对数量。特别地，第一行表示初始集合 $A$ 和 $B$ 的结果。

6
1 2
2 3
3 4
3 5
5 6
1 2 1
1
5 6
A + 2

1
3

提示

样例 1 解释

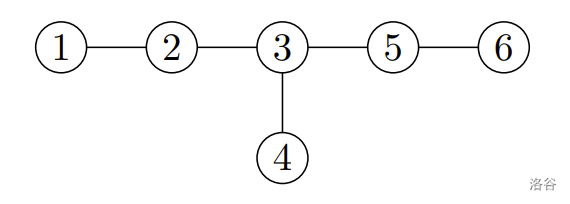
初始时，$A=\{1\}, B=\{5, 6\}$，可选初始对 $(a, b)$ 为 $(1, 5)$ 和 $(1, 6)$。

• 对 $(1, 5)$：玩家一涂格子 $2$，玩家二涂格子 $3$，玩家一无格子可涂，输。
• 对 $(1, 6)$：玩家一涂格子 $2$，玩家二涂格子 $5$，玩家一涂格子 $3$，玩家二无格子可涂，输。
  仅 $(1, 6)$ 使玩家一获胜，输出 $1$。

更新后，$A=\{1, 2\}, B=\{5, 6\}$，玩家一在 $(1, 5), (2, 5), (2, 6)$ 有制胜策略，输出 $3$。

附加样例

1. $n=10, q=0$，格子 $i>1$ 连接格子 $1$，$A=\{1, 2, 3\}, B=\{4, 5, 6\}$，答案为 $9$。
2. $n=200, q=0$，格子 $i>1$ 连接格子 $i-1$，$A=\{1, 2, 3\}, B=\{1, 2, 3\}$，答案为 $3$。
3. $n=2000, q=0$，格子 $i>1$ 连接格子 $\lfloor i/2 \rfloor$，$A=B=\{1, 2, \ldots, n\}$，答案为 $2411948$。
4. $n=500000, q=0$，格子 $i>1$ 连接格子 $\lfloor i/2 \rfloor$，$A=B=\{1, 2, \ldots, n\}$，答案为 $150744198828$。
5. $n=500000, q=1$，格子 $i>1$ 连接格子 $i-1$，$A=\{1, 2, 3\}, B=\{1\}$，更新移除 $B$ 的格子 $1$。
6. $n=500000, q=1$，格子 $i>1$ 连接格子 $i-1$，$A=\{1, 2, 3\}, B=\{1, 2, 3\}$，更新移除 $B$ 的格子 $3$。

详细子任务附加限制及分值如下表所示。

子任务编号	附加限制	分值
$1$	$q=0, n \leq 10$	$8$
$2$	$q=0, n \leq 200$	$10$
$3$	$q=0, n \leq 2000$	$18$
$4$	$q=0$	$30$
$5$	$z=\texttt{B}$	$16$
$6$	无附加限制	$18$