题目描述

You are given a set of $n$ segments on a line $[L_i; R_i]$. All $2n$ segment endpoints are pairwise distinct integers.

The set is $\emph{laminar}$ --- any two segments are either disjoint or one of them contains the other.

Choose a non-empty subsegment $[l_i, r_i]$ with integer endpoints in each segment ($L_i \le l_i < r_i \le R_i$) in such a way that no two subsegments intersect (they are allowed to have common endpoints though) and the sum of their lengths ($\sum_{i=1}^n r_i - l_i$) is maximized.

输入格式

The first line contains a single integer $n$ ($1 \le n \le 2 \cdot 10^3$) --- the number of segments.

The $i$-th of the next $n$ lines contains two integers $L_i$ and $R_i$ ($0 \le L_i < R_i \le 10^9$) --- the endpoints of the $i$-th segment.

All the given $2n$ segment endpoints are distinct. The set of segments is laminar.

输出格式

On the first line, output the maximum possible sum of subsegment lengths.

On the $i$-th of the next $n$ lines, output two integers $l_i$ and $r_i$ ($L_i \le l_i < r_i \le R_i$), denoting the chosen subsegment of the $i$-th segment.

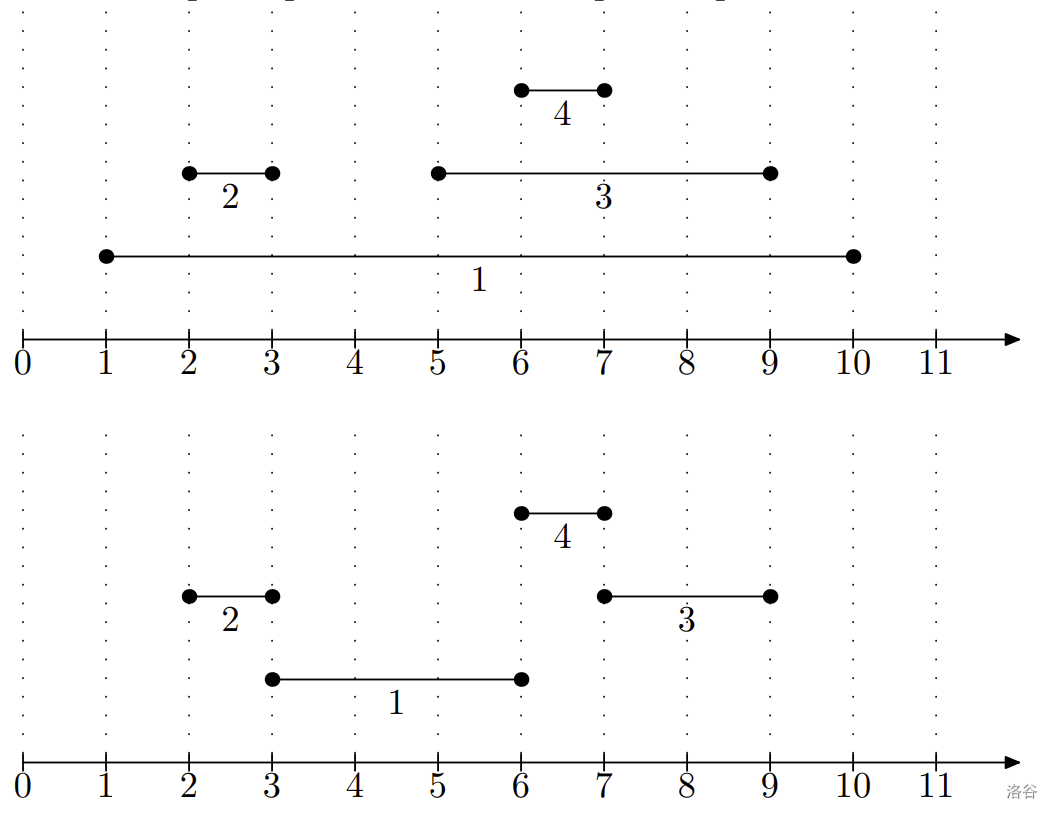
4
1 10
2 3
5 9
6 7

7
3 6
2 3
7 9
6 7

提示

The example input and the example output are illustrated below.