题目描述

A city skyline is specified by $n$ integers $d_1, d_2, \ldots, d_n$ ($0 < d_1 < d_2 < \ldots < d_n$) and $n$ integers $h_1, h_2, \ldots, h_n$.

A skyline surface consists of $n$ horizontal line segments, the $i$-th segment connects points $(d_{i-1}, h_i)$ and $(d_i, h_i)$, where $d_0 = 0$. Each segment is a roof of a building.

A cat (which is so small that can be considered a point) wants to get from the leftmost point of the skyline, $(0, h_1)$, to the rightmost point of the skyline, $(d_n, h_n)$. To achieve that, the cat performs a sequence of moves. Each move is one of two types:

• $\emph{Walk}$ from point $(x_1, y_1)$ to point $(x_2, y_2)$. Both points must belong to the same surface segment, i.e. there exists $i$ such that $y_1 = y_2 = h_i$ and $d_{i-1} \le x_1, x_2 \le d_i$. A trajectory of a walk is a straight line segment.
• $\emph{Jump}$ from point $(x_1, y_1)$ to point $(x_2, y_2)$. Points $(x_1, y_1)$ and $(x_2, y_2)$ must belong to different surface segments. A trajectory of a jump is a straight line segment and must satisfy the following constraints:
  • the distance between $(x_1, y_1)$ and $(x_2, y_2)$ is at most $L$;
  • the line segment between $(x_1, y_1)$ and $(x_2, y_2)$ does not intersect any of the buildings, i.e. thereis no point $(x, y)$ belonging to the segment and integer $i$ such that $d_{i-1} < x < d_i$ and $y < h_i$.

The length of the cat's trajectory is the sum of lengths of all the moves in it. Find the shortest trajectory for the cat to get from $(0, h_1)$ to $(d_n, h_n)$, or determine that the goal is unreachable.

输入格式

The first line contains two integers $n$ and $L$ ($1 \le n \le 50$; $1 \le L \le 100$).

The second line contains $n$ integers $d_1, d_2, \ldots, d_n$ ($0 < d_1 < d_2 < \ldots < d_n \le 1000$).

The third line contains $n$ integers $h_1, h_2, \ldots, h_n$ ($1 \le h_i \le 100$; $h_i \ne h_{i+1}$).

输出格式

Output a single floating-point number --- the length of the shortest trajectory from point $(0, h_1)$ to point $(d_n, h_n)$, or $-1$ if no valid trajectory exists.

Your answer will be considered correct if its absolute or relative error doesn't exceed $10^{-9}$.

6 5
3 9 11 12 16 18
5 1 6 2 5 7

25.83095189484530047

6 4
3 9 11 12 16 18
5 1 6 2 5 7

-1

提示

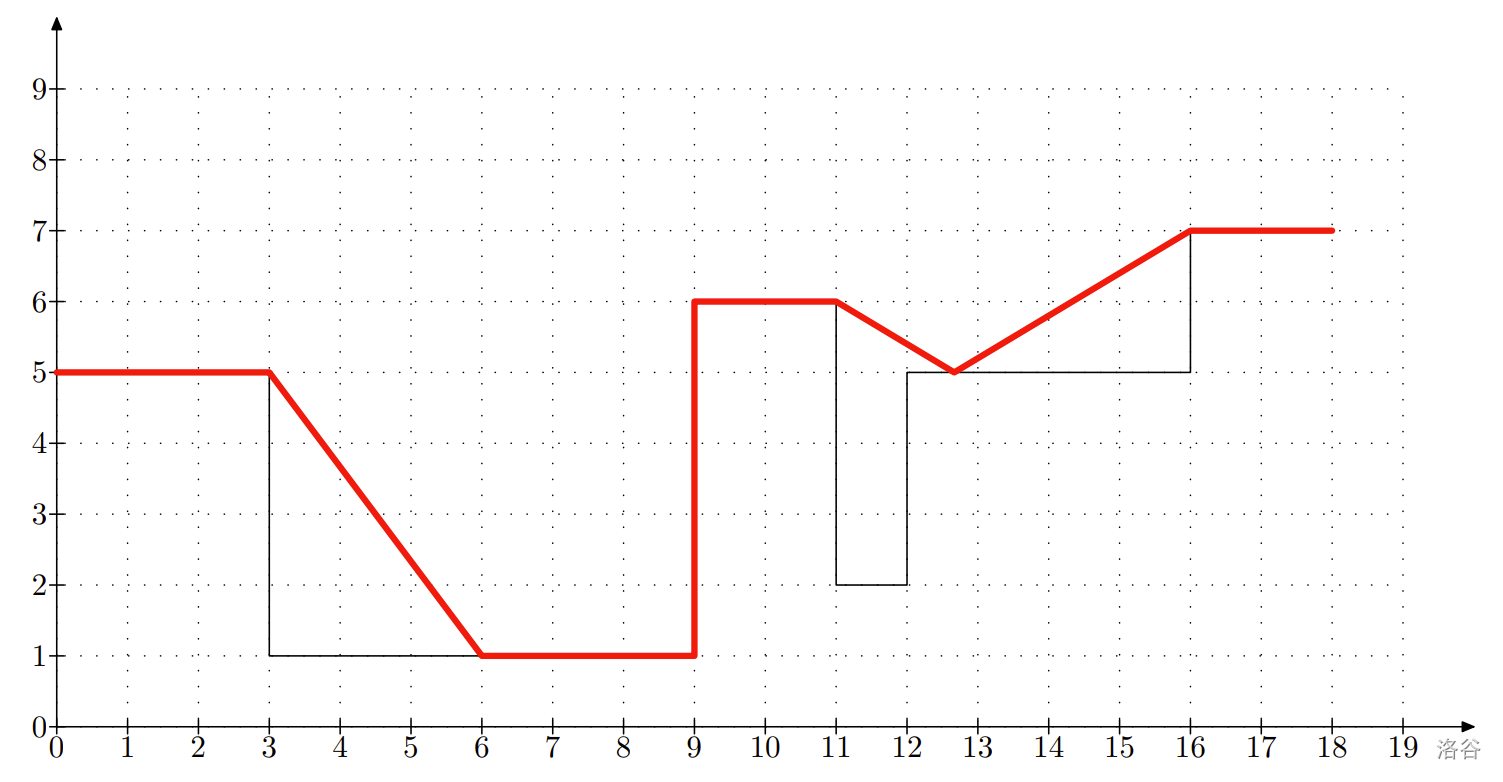
The picture for the first sample is shown below.