题目描述

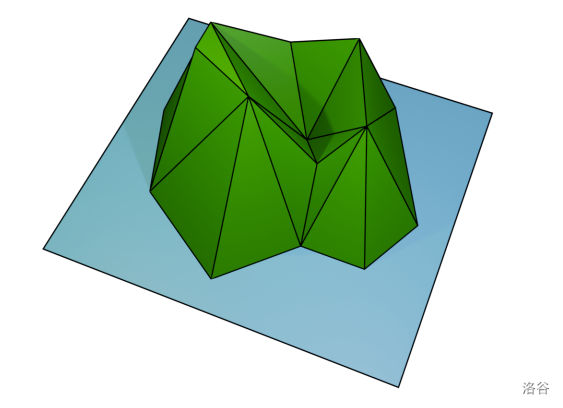
You are developing a new computer game. Let's consider an island in the middle of the ocean in a three-dimensional space with $z$-axis pointing upwards. The surface of the ocean is a horizontal plane with $z = 0$. The island is a polyhedron of a special form.

You are given $n$ points $(x_i, y_i, z_i)$; there are some edges between them. If we look at the island from above or if we discard $z$ coordinate of each point, points and edges form a planar connected graph. Every face of this planar graph, except the external one, is a nondegenerate triangle. Every edge of the graph belongs to at least one internal face. All points that lie on the edge of the external face of the graph have $z$ coordinates equal to zero. Other points may have arbitrary non-negative $z$ coordinates. Every face of the planar graph corresponds to the face of the polyhedron with the same vertices.

Due to global warming, the level of the ocean is increasing and floods the island. Your task is to compute various global warming scenarios for the game.

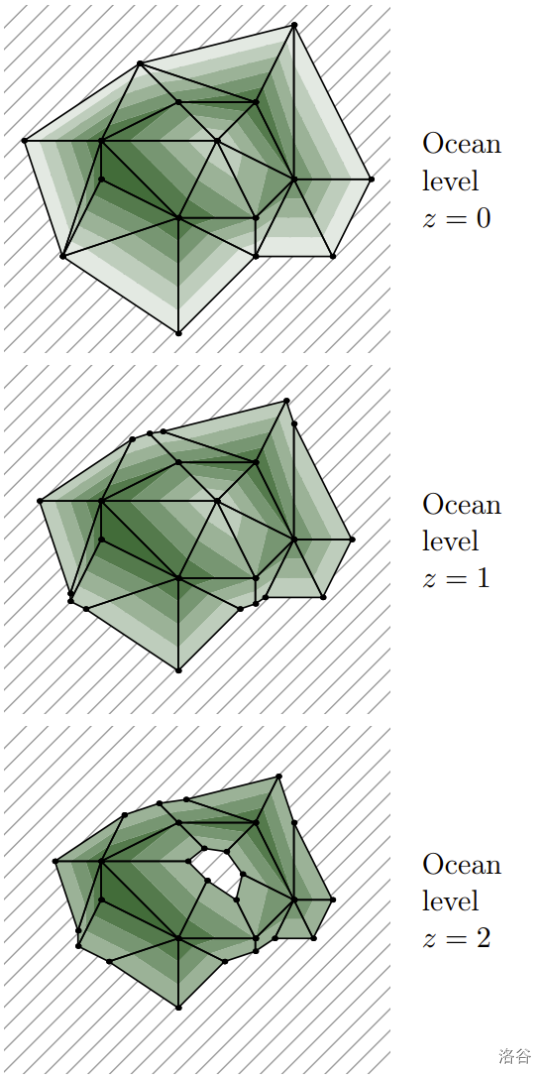
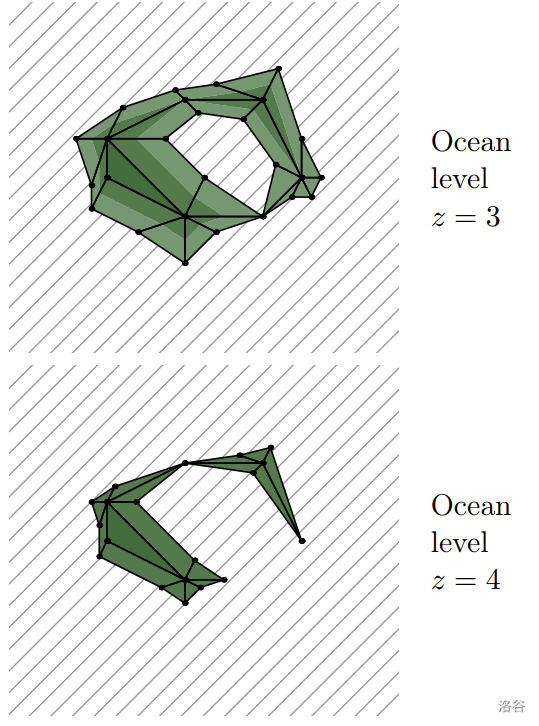
In each scenario, the level of the ocean increased to the height $h$, so that the surface of the ocean is a plane $z = h$. Parts of the island that are $\textbf{below or at the height h}$ are now $\textit{flooded}$, even though some parts may be not reachable from the ocean by water (see the illustration for the second example). In a scenario, a player is standing in $p$-th point. You shall compute the area of the surface of the part of the island where the player is standing, or determine that the player is standing at or below the water level and has drowned.

Formally, we say that two points on the surface of the island belong to the same part if a player can move between them walking by the surface of the island staying strictly higher than ocean level. Note that you should find the area of the surface of the island itself, not the area of its projection on a horizontal plane.

输入格式

The first line contains a single integer $n$ --- the number of points ($1 \le n \le 10^5$).

Each of the next $n$ lines contains three integers $x_i$, $y_i$, and $z_i$ --- the coordinates of $i$-th point ($-10^6 \le x_i, y_i \le 10^6$; $0 \le z_i \le 10^6$).

The next line contains a single integer $m$ --- the number of internal faces of the planar graph ($1 \le m \le 10^5$). They are also the faces of the island's polyhedron.

Each of the next $m$ lines contains three integers $a_i$, $b_i$, and $c_i$ --- the indices of three points that are vertices of $i$-th internal face ($1 \le a_i, b_i, c_i \le n$).

It is guaranteed that if $z$ coordinate is discarded, then the resulting graph is a connected and planar graph. All its faces, except the external one, are nondegenerate triangles. All points that lie on the edge of the external face of the planar graph have $z$ coordinate equal to zero.

The next line contains an integer $q$ --- the number of global warming scenarios to compute ($1 \le q \le 10^5$).

Each of the next $q$ lines contains two integers $h_i$ and $p_i$ --- the level of the ocean and the index of the point where the player is standing respectively ($0 \le h_i \le 10^6$; $1 \le p_i \le n$).

输出格式

For every scenario output a single real number --- the area of the surface of part of the island where the player is standing. If the player's position is flooded by water, output $-1$ instead.

The answer is considered correct if its absolute or relative error does not exceed $10^{-6}$.

5
0 0 0
2 0 0
2 2 0
0 2 0
1 1 4
4
1 2 5
2 3 5
3 4 5
4 1 5
7
0 1
0 5
1 5
2 5
3 5
4 5
5 5

-1
16.492422502470642
9.276987657639736
4.123105625617661
1.030776406404415
-1
-1

16
0 5 0
1 2 0
2 5 5
3 7 0
4 0 0
4 3 5
5 5 1
6 2 0
6 6 5
7 4 4
7 8 0
8 2 0
9 4 0
4 6 4
6 3 3
2 4 5
22
11 10 9
12 8 10
2 6 5
9 10 7
8 15 6
16 3 6
15 6 7
7 3 14
8 10 15
11 13 10
16 6 2
12 10 13
10 7 15
16 3 2
3 4 1
14 7 9
11 9 4
3 6 7
5 6 8
14 4 3
3 1 2
9 4 14
7
0 7
1 7
1 16
2 10
3 9
4 16
5 16

120.483405354306325
-1
93.929895222484783
68.181919663536940
40.918561474148331
11.067441790921070
-1

提示

The illustrations of the examples are views of the island from the above. The ocean is hatched. The island is drawn with contour lines, with higher parts in darker colors.

Sample 1

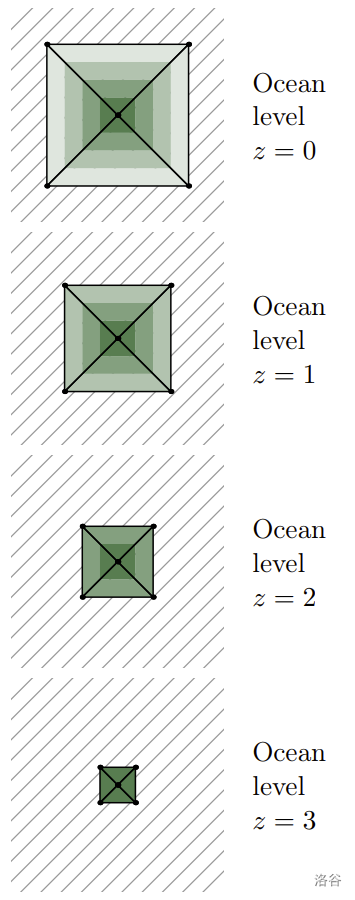
Sample 2

The island in the second example looks as follows.