题目描述

Alice has a nice cactus graph that she wanted to place on a sheet of paper. Eve threatens to take one cycle of this cactus and cut the paper along all edges on this cycle. This way, the sheet of paper will be divided in two parts, and Alice will be upset. Luckily, Barbara just gave Alice a paper torus --- a sheet of paper where top and bottom edges are connected as well as left and right edges are connected without twisting. On torus, you can sometimes cut paper along all edges on a cycle, but it would still remain in one piece. Help Alice to determine if she can place her cactus on a torus such that Eve cannot cut paper along one cycle dividing the torus into two unconnected pieces.

$\textit{Cactus}$ is a connected undirected graph in which every edge lies on at most one simple cycle. Intuitively, cactus is a generalization of a tree where some cycles are allowed. Multiedges (multiple edges between a pair of vertices) and loops (edges that connect a vertex to itself) are not allowed in a cactus.

We say that a graph is placed on a sheet of paper if each vertex is a point on this sheet, each edge is a segment between points corresponding to its vertices, and these segments only intersect at their ends. On torus segments can go through sheet edges any number of times.

输入格式

The input consists of one or more independent test cases.

The first line of each test case contains two integers $n$ and $m$ ($1 \le n \le 10^5$; $0 \le m \le 10^5$), where $n$ is the number of vertices in the graph. Vertices are numbered from $1$ to $n$. The edges of the graph are represented by a set of edge-distinct paths, where $m$ is the number of such paths.

Each of the following $m$ lines contains a path in the graph. A path starts with an integer $s_i$ ($2 \le s_i \le 1000$) followed by $s_i$ integers from $1$ to $n$. These $s_i$ integers represent vertices of a path. Adjacent vertices in a path are distinct. The path can go through the same vertex multiple times, but every edge is traversed exactly once in the whole test case. There are no multiedges in the graph (there is at most one edge between any two vertices).

The last line of the input after all test cases contains two zeros. It does $\textbf{not}$ define a test case. It just marks the end of the input and does not require any output.

All graphs in the input are cacti. The total sum of all values of $n$ and the total sum of all values of $m$ throughout the input both do not exceed $10^5$.

输出格式

Print the answer for each test case in the same order the cases appear in the input. For each test case, print a single line with Yes if you can place this cactus on a torus or print No otherwise.

6 1
8 1 2 3 1 4 5 6 4
10 2
9 1 2 3 1 10 4 5 6 4
5 7 8 9 7 10
0 0

Yes
No

提示

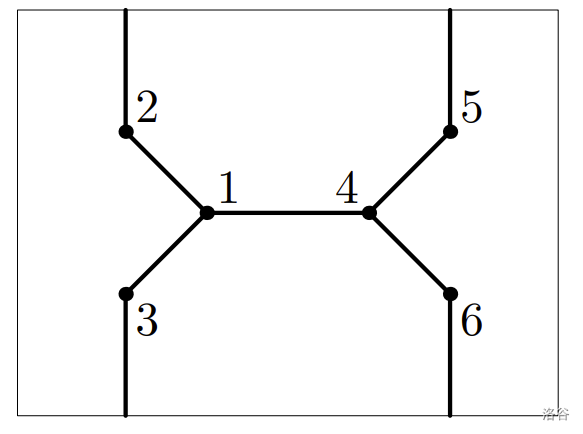
One way to place the cactus from the first case on a torus is shown on the picture.