题目背景

译自 ICPC 2024 Yokohama Regional Contest。

题目描述

国际解析竞赛的一道题引起了你的注意。

给定两个表达式作为输入，每个表达式表示生成一棵树的过程。 生成过程是随机化的，这意味着每次执行该过程可能生成不同的树。你需要计算两个表达式各自可能生成的树的交集的大小。

表达式的语法如下：

$$ E ::= \texttt{‘1’} \operatorname{|} \texttt{‘(’}E \, E \texttt{‘)’} $$

根据以下过程，从一个表达式生成一棵树。

• 表达式 $\texttt{1}$ 生成一棵仅包含一个标号为 $1$ 的节点的树。
• 对于两个表达式 $E_1$ 和 $E_2$，表达式 $(E_1E_2)$ 按如下方式生成一棵树：
  1. 从 $E_1$ 生成一棵拥有 $n_1$ 个节点的树 $T_1$，并从 $E_2$ 生成一棵拥有 $n_2$ 个节点的树 $T_2$。
  2. 将 $T_2$ 中所有节点的标号都加上 $n_1$。
  3. 随机地各从 $T_1$ 和 $T_2$ 中选取一个节点，连接它们形成一条边，从而构造出一棵标号为 $1$ 到 $(n_1 + n_2)$ 的树，该树即为 $(E_1E_2)$ 生成的树。

例如，表达式 $\texttt{(11)}$ 只能生成下图中最左边的树，而 $\texttt{(1(11))}$ 可以生成其余两棵树。

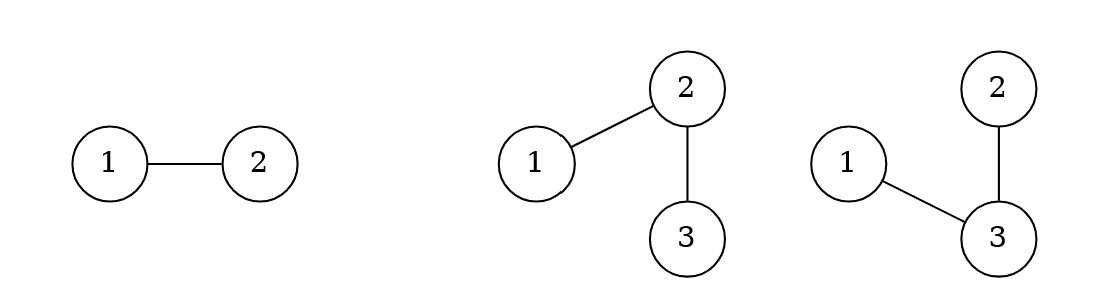
相同的树可能由不同的表达式生成。中间的那棵树也可以由 $\texttt{((11)1)}$ 生成。

对于给定的两个长度相同的表达式，计算它们都能生成的树的数量。注意，它们生成的树节点数总是相同的。如果存在两个数 $i$ 和 $j$，使得在一棵树中标号 $i$ 和 $j$ 的节点之间有一条边，而在另一棵树中没有，则这两棵树被视为不同。

输入格式

输入共两行，每行一个表达式串。两个字符串长度相同，范围在 $1$ 到 $7\times10^5$（含两端）之间，且符合上述语法。

输出格式

输出两个表达式都能生成的树的数量，对 $998\,244\,353$ 取模。

((1(11))1)
((11)(11))

1

(1(11))
(1(11))

2

(((11)(11))((11)1))
((1(11))(1(1(11))))

3

((11)(((1(11))1)((11)1)))
(1(((11)((11)(11)))(11)))

4

提示

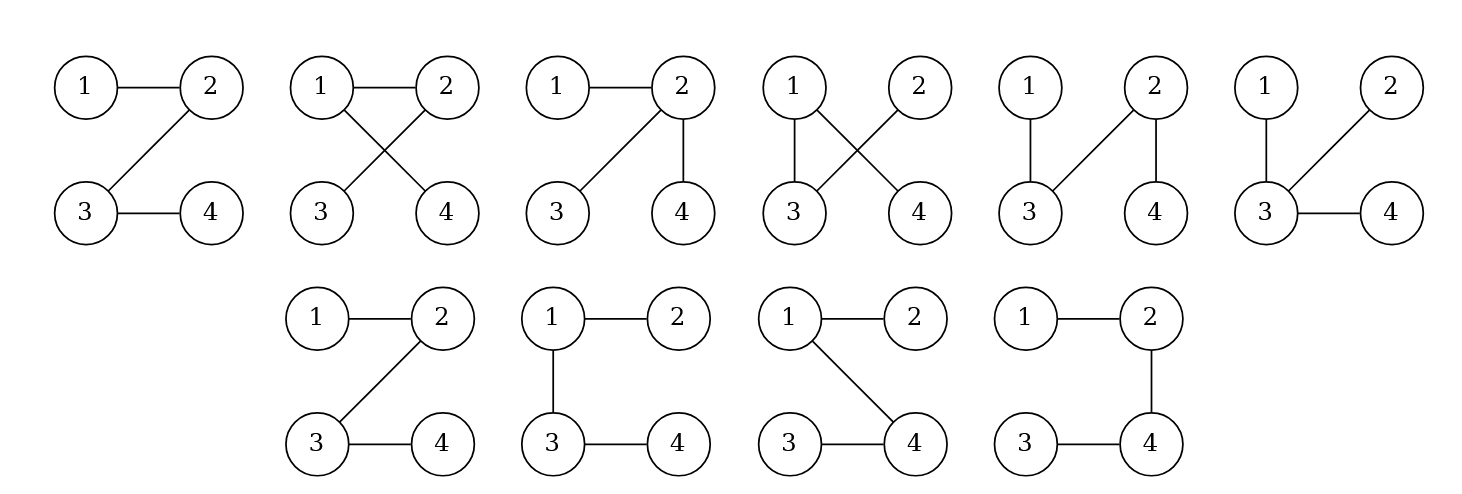
对于样例 $1$，可生成的树如下图所示。上排六棵对应第一个表达式，下排四棵对应第二个表达式。仅每行最左边的那棵树可由两者共同生成。