题目背景

翻译来自于 LibreOJ。

题目描述

题目译自 XXV Olimpiada Informatyczna — III etap Ogrodzenie

农夫 Bajtazar 刚购置了一块土地，上面生长着 $n$ 株植物。其中一些是果树，每年带来非负收益（果实价值不等）；另一些是杂草，只会造成损失（占用空间和阳光）。

Bajtazar 为每株植物估算了留下它的收益或损失。然而，拜托尼亚禁止破坏自然，他无法随意移除带来损失的植物。幸好，他需为土地建围栏，于是突发奇想：何必围住整块土地？只围住收益最大的部分即可！

Bajtazar 请你帮忙设计最优围栏。围栏需经济高效：他将选择部分植物，用弹性网固定于其上，围成的区域必须是面积大于 $0$ 的凸多边形。请帮助 Bajtazar 挑选支撑网的植物，最大化围栏内植物的收益总和。

输入格式

第一行包含一个整数 $n$ $(n \geq 3)$，表示土地上植物数量。

接下来的 $n$ 行描述各植物，第 $i$ 行包含三个整数 $x_i, y_i, v_i$ $(-10^9 \leq x_i, y_i \leq 10^9, -10^9 \leq v_i \leq 10^9)$，分别表示第 $i$ 株植物在直角坐标系中的位置 $(x_i, y_i)$ 及其收益（若 $v_i$ 为负则为损失）。保证任意三株植物不在同一直线上。

输出格式

输出一行，包含一个整数，表示围栏内植物可实现的最大收益总和。

6
0 0 1
0 4 1
4 0 1
4 4 1
1 2 -1
2 6 -5

3

提示

样例 1 解释

图示展示了一种最大收益为 $3$ 的围栏设置。另一种同样最优的方案是固定网于点 $(0,0), (4,0), (4,4)$ 的植物。

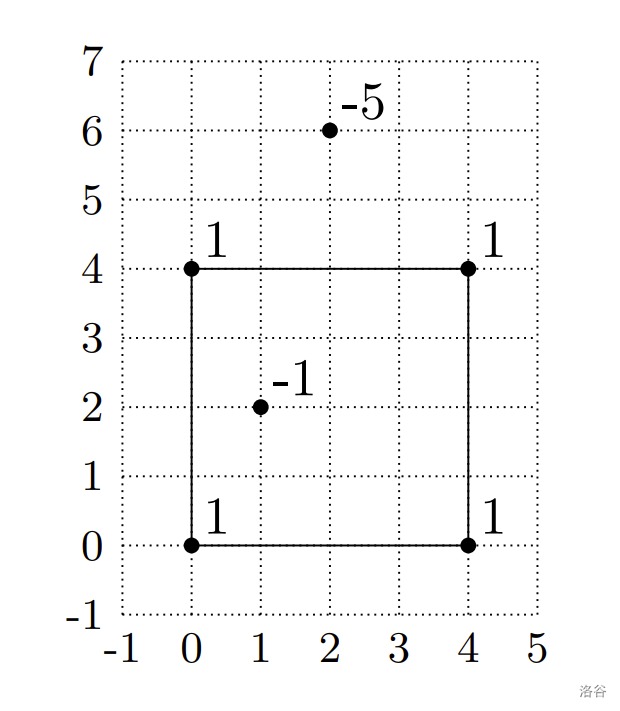
附加样例

1. $n=8$，围住所有植物最优。
2. $n=100, x_i=i, y_i=i^2 \bmod 101, v_i=50-i$，植物排列形似甲虫。
3. $n=300$，植物构成凸多边形顶点，每隔一株收益 $1$，另一株损失 $1$。

详细子任务附加限制及分值如下表所示。