题目背景

翻译来自于 LibreOJ。

题目描述

题目译自 XXV Olimpiada Informatyczna — III etap Dwa pionki

在无限网格的点 $(0,0)$ 上放置了两个棋子。每个棋子有 $n$ 种允许的移动方式（两棋子移动方式相同）。每种移动由一个整数组成的向量描述。每个棋子可将每种移动使用至多一次，顺序任意。两棋子可执行相同的移动。描述移动的向量可能重复，每棋子可使用每个重复向量。

目标是移动棋子，使两者间的欧几里得距离尽可能大。求这一最大距离的平方。

输入格式

第一行包含一个正整数 $n$，表示棋子的移动方式数量。

接下来的 $n$ 行，每行包含两个整数 $x_i, y_i$ $(-10^4 \leq x_i, y_i \leq 10^4)$，表示描述棋子移动的向量 $[x_i, y_i]$。

输出格式

输出一个整数，表示可使两棋子相距最大距离的平方。

3
-1 3
-1 -2
4 0

41

提示

样例 1 解释

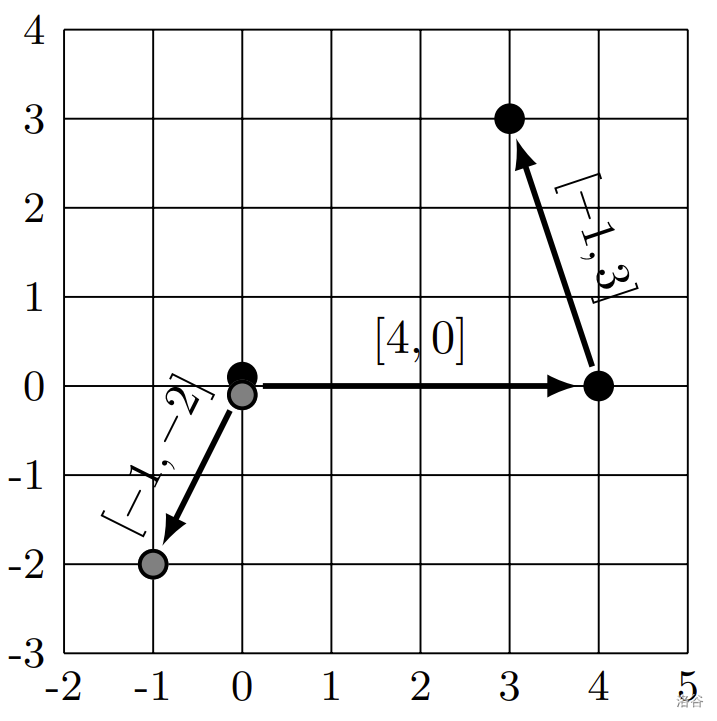
图示展示了最优解：第一个棋子执行向量 $[4,0]$ 和 $[-1,3]$ 的移动，第二个棋子执行向量 $[-1,-2]$ 的移动。

附加样例

1. $n=5$，向量为 $[0,0], [1,0], [0,-1], [-1,0], [0,1]$。
2. $n=100$，向量为 $[i,j]$，其中 $i,j \in \{1,2,\ldots,10\}$。
3. $n=200000$，所有向量为 $[-1,-1]$。

详细子任务附加限制及分值如下表所示。