题目背景

翻译来自于 LibreOJ。

题目描述

题目译自 XXV Olimpiada Informatyczna — II etap Drogi rowerowe

拜托城国王 Bajtazar 倾听民意，决定将部分预算盈余用于修建自行车道。皇家道路顾问已设计了一套单向自行车道网络，连接各路口，但经国王要求进行了多次修改。网络由连接路口 $u$ 到 $v$ 的单向路段组成。从路口 $u$ 到 $v$ 的路径定义为任意一串不同路口序列 $u=v_0, v_1, \ldots, v_k=v$，其中每对连续路口 $v_i, v_{i+1}$ $(0 \leq i < k)$ 由从 $v_i$ 到 $v_{i+1}$ 的路段连接。

国王要求网络「公平」，即满足：若从路口 $v$ 无法到达路口 $u$（不存在从 $v$ 到 $u$ 的路径），则从 $u$ 到 $v$ 至多只有一条路径。国王认为，这能避免路口 $v$ 的居民嫉妒路口 $u$ 的居民。

市民自行车委员会获取了这一公平网络的设计，却对此不满，认为它不便于城市出行。他们需提交报告，急需确凿数据。你需计算网络的通达度，即对于每个路口 $v$，计算从 $v$ 可达的路口数量。

输入格式

第一行包含两个整数 $n, m$ $(n \geq 2, m \geq 1)$，分别表示拜托城的路口数量和路段数量，路口编号为 $1$ 至 $n$。

接下来的 $m$ 行描述网络，每行包含两个整数 $a, b$ $(1 \leq a, b \leq n, a \neq b)$，表示存在从路口 $a$ 到 $b$ 的单向路段。每对有序对 $(a, b)$ 至多出现一次，保证网络公平。

输出格式

输出 $n$ 行，第 $i$ 行包含一个整数，表示从路口 $i$ 可达的路口数量。

7 7
1 4
1 6
4 2
6 2
2 1
5 3
3 7

3
3
1
3
2
3
0

提示

样例 1 解释

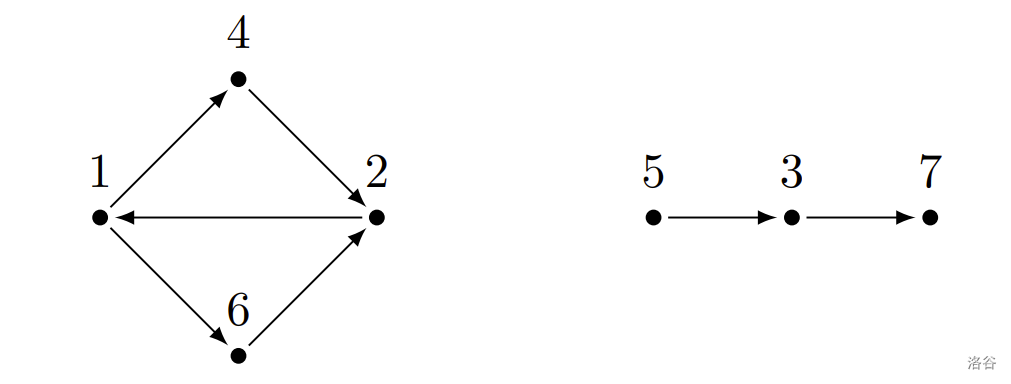
附加样例

1. $n=25, m=600$，每路口到其他路口均有路段。
2. $n=55, m=54$，含孤立路口及长度 $2$ 至 $10$ 的独立环。
3. $n=50000, m=49999$，所有路口在一条路径上。
4. $n=50000, m=50000$，所有路口在一个环上。

详细子任务附加限制及分值如下表所示。