题目背景

翻译来自于 LibreOJ。

题目描述

题目译自 XXIII Olimpiada Informatyczna — III etap Niebanalne podróże

Bajtazar 最近迷上了在拜托尼亚的旅行。拜托尼亚有 $n$ 座城市（为方便起见，编号为 $1$ 至 $n$），铁路系统提供 $m$ 条双向铁路连接部分城市对。借助这些铁路，Bajtazar 可到达每座城市（可能需要换乘）。

他尤其钟情于一种非凡旅行：从某城市出发，最终返回起点，途中不重复访问任何城市，也不重复使用任何铁路。这种旅行他称之为非凡。

在一次旅行中，Bajtazar 注意到，每次非凡旅行使用的铁路条数相同。他怀疑这是拜托尼亚铁路网络的普遍特性，请你帮助验证这一猜想。若猜想正确，他还想知道非凡旅行的数量。由于答案可能很大，他只需知道数量对 $10^9+7$ 取模的结果。

旅行可用依次访问城市的编号序列描述。两条同等长度的旅行若存在某位置 $i$，其第 $i$ 个访问城市不同，则视为不同。旅行长度指使用的铁路条数。

输入格式

第一行包含两个整数 $n, m$ $(n \geq 1, m \geq 0)$，分别表示拜托尼亚的城市数量和铁路连接数量。

接下来的 $m$ 行描述铁路连接，第 $i$ 行包含两个整数 $a_i, b_i$ $(1 \leq a_i, b_i \leq n, a_i \neq b_i)$，表示城市 $a_i$ 和 $b_i$ 间存在双向铁路。每对城市间至多有一条直接铁路。

输出格式

若不存在任何非凡旅行，输出一行，包含字符串 BRAK。

若存在非凡旅行，但长度不尽相同（即 Bajtazar 的猜想错误），输出一行一个字符串 NIE。

若所有非凡旅行长度相同（即猜想正确），输出一行一个字符串 TAK；下一行输出两个整数，分别表示非凡旅行的长度和旅行数量对 $10^9+7$ 取模的结果。

5 6
1 2
2 3
3 1
1 4
4 5
5 1

TAK
3 12

12 14
1 2
2 4
3 1
4 3
4 5
5 6
6 7
7 8
8 4
7 9
9 12
12 11
11 10
10 6

NIE

提示

样例 1 解释

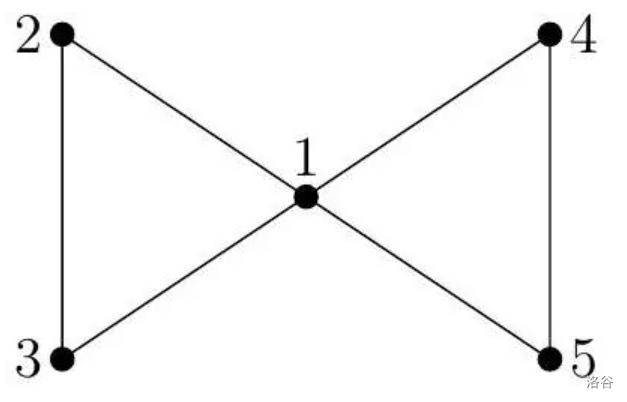
所有非凡旅行长度为 $3$，共 $12$ 条，依次为 $1-2-3-1, 1-3-2-1, 2-1-3-2, 2-3-1-2, 3-1-2-3, 3-2-1-3,$ $1-4-5-1, 1-5-4-1, 4-1-5-4, 4-5-1-4, 5-1-4-5, 5-4-1-5$。

样例 2 解释

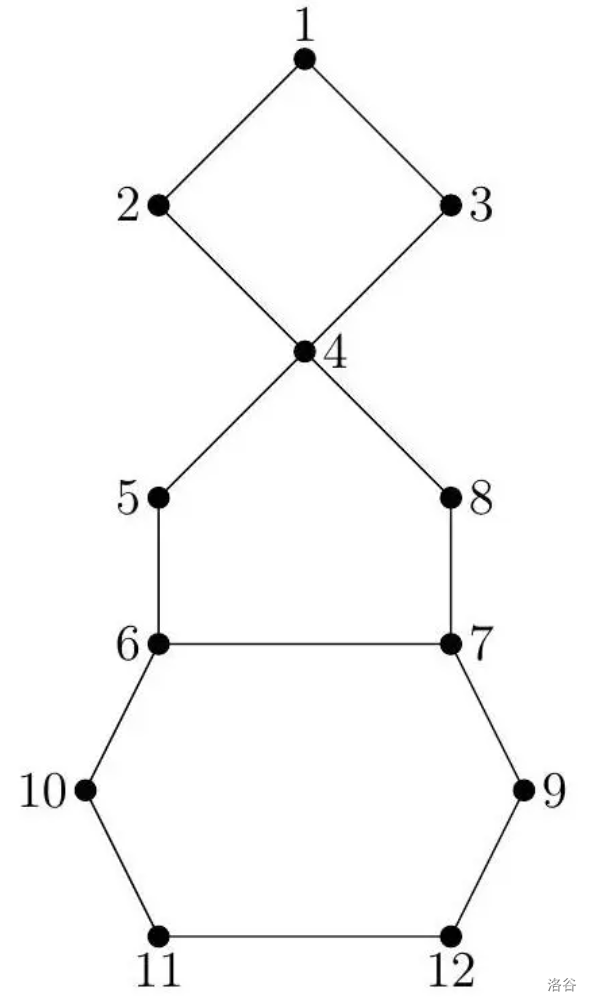
附加样例

1. $n=500000$，城市呈路径状，答案为 BRAK。

详细子任务附加限制及分值如下表所示。