题目背景

翻译来自于 LibreOJ。

题目描述

题目译自 XXIII Olimpiada Informatyczna — II etap Drogi zmiennokierunkowe

Bajtazar 正考虑搬到巴厘城，计划在那里租一间公寓。巴厘城是一座充满魅力的城市，拥有诸多优点，但交通便利性却不在此列。城中有 $n$ 个路口，通过 $m$ 条略显杂乱的单行道连接。由于道路狭窄，出于实际需要，所有道路均为单向通行。然而，当地交通专家提出了一种巧妙的解决方案，无需拓宽道路即可实现双向通行：每天早晨，所有道路的通行方向都会切换。也就是说，在奇数日期，车辆按道路的原始方向行驶；而在偶数日期，所有道路方向反转。

Bajtazar 希望租住在一处交通便利的公寓，具体来说，他想选择一个路口，从那里出发，能在一天内（奇数日或偶数日）到达城内任意其他路口。他并不担心返程问题，因为他可以在次日返回。

给定巴厘城的道路网络，请找出所有满足 Bajtazar 要求的路口。

输入格式

第一行包含两个整数 $n, m$ $(n \geq 2, m \geq 1)$，分别表示巴厘城的路口数量和道路数量。路口编号为 $1$ 至 $n$。

接下来的 $m$ 行，每行包含两个整数 $a_i, b_i$ $(1 \leq a_i, b_i \leq n, a_i \neq b_i)$，表示存在一条单行道，在奇数日期从路口 $a_i$ 通向路口 $b_i$，在偶数日期从 $b_i$ 通向 $a_i$。每对有序对 $(a_i, b_i)$ 在输入中至多出现一次。

输出格式

第一行输出一个整数 $k$，表示满足 Bajtazar 要求的路口数量。

第二行输出 $k$ 个递增的整数，表示这些路口的编号，数字间用单个空格分隔。若 $k=0$，第二行应为空（可输出空行或省略）。

6 7
1 2
1 3
2 4
3 4
4 5
5 6
6 5

4
1 4 5 6

提示

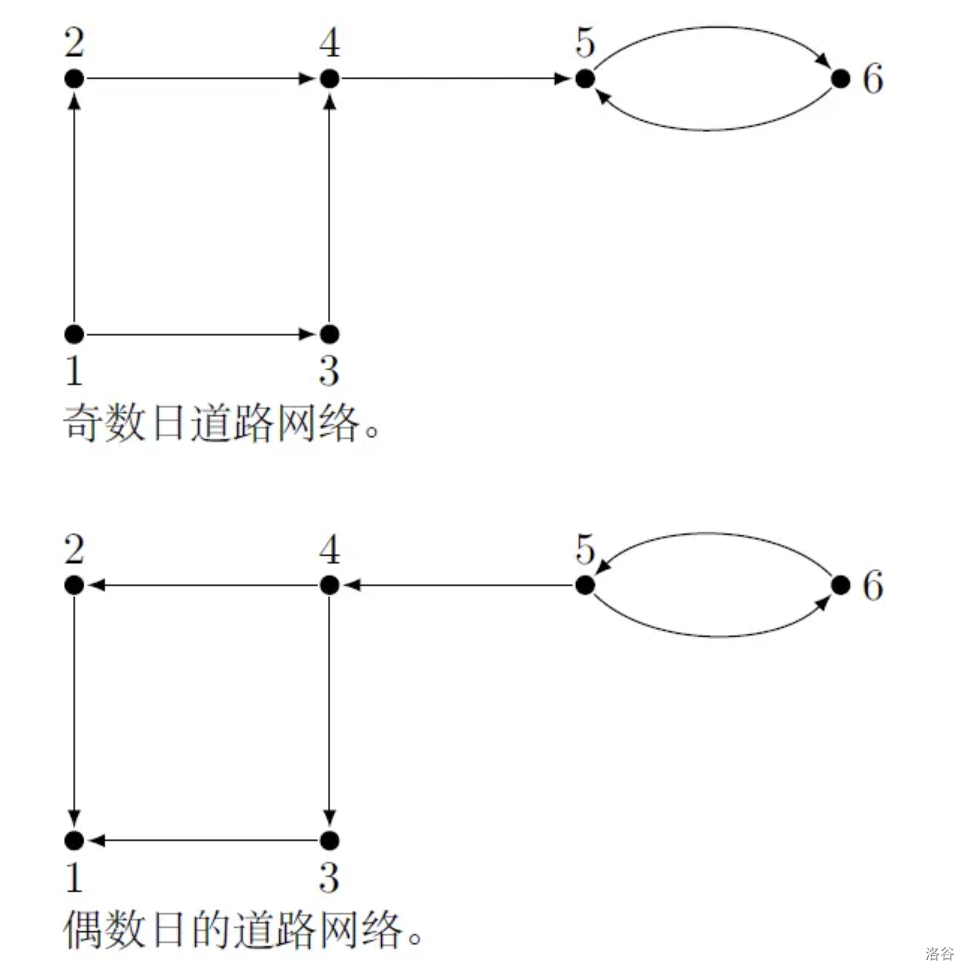
样例 1 解释

从路口 $1$ 出发，在奇数日期可到达所有其他路口。从路口 $5$ 和 $6$ 出发，在偶数日期可到达所有其他路口。从路口 $4$ 出发，在奇数日期可到达路口 $5$ 和 $6$，在偶数日期可到达路口 $1, 2, 3$。

附加样例

1. $n=10, m=9$，道路构成一条交替路径，每隔一条道路方向向左或向右，无路口满足要求。
2. $n=100000, m=100000$，奇数日期从路口 $1$ 可直达所有其他路口，且从路口 $n$ 可直达路口 $1$，仅路口 $1$ 和 $n$ 满足要求。
3. $n=500000, m=499999$，一条路径，所有路口均满足要求。

详细子任务附加限制及分值如下表所示。