题目描述

小 Z 想用大小为 $1\times2$ 的骨牌覆盖大小为 $n\times m$ 的棋盘，要求棋盘上的每个位置都要被覆盖并且骨牌没有重叠。他认为两块骨牌的短边拼在一起是不好看的，所以他不允许这种情况出现。现在小 Z 已经把棋盘边缘的一圈骨牌放好了，请你求出用骨牌覆盖剩下的区域的方案数。答案可能很大，你只需要求出其对 $998244353$ 取模的结果。

输入格式

第一行三个整数 $n,m,k$。其中 $k$ 表示小 Z 已经放置的骨牌数量。

接下来 $k$ 行，每行三个整数 $x,y,t$。表示已经有一块被放置的骨牌左上角在棋盘的第 $x$ 行第 $y$ 列，如果 $t=1$ 则表示这块骨牌是横向放置的，如果 $t=2$ 则表示这块骨牌是纵向放置的。

输出格式

输出一行一个整数即答案。

1 4 2
1 1 1
1 3 1

0

5 6 12
1 1 2
1 2 2
1 3 1
1 5 2
1 6 2
3 1 1
3 5 1
4 1 2
4 2 2
4 5 2
4 6 2
5 3 1

2

6 6 14
1 1 2
1 2 2
1 3 1
1 5 2
1 6 2
3 1 1
3 5 1
4 1 1
4 5 1
5 1 2
5 2 2
5 5 2
5 6 2
6 3 1

1

提示

样例解释

在第一组样例中，小 Z 在棋盘上放置的骨牌如下图所示：

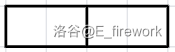
放置的两块骨牌短边相接，是不合法的，所以方案数为 $0$。

---

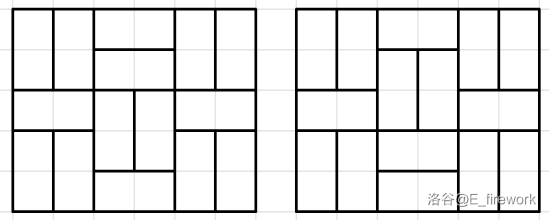
在第二组样例中，小 Z 在棋盘上放置的骨牌如下图所示：

有以下两种合法的方案：

---

在第三组样例中，小 Z 在棋盘上放置的骨牌如下图所示：

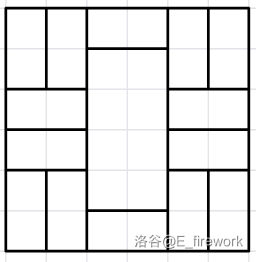
只有一种合法的方案：

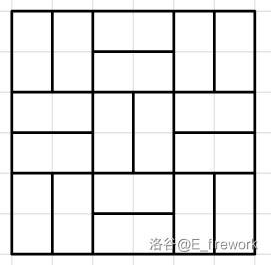
数据范围与约定

本题使用捆绑测试。

对于 $100\%$ 的数据，保证 $1\le n,m\le5\times10^5$，$\frac{3}{2}(n+m-200)\le k\le2(n+m)$，已经放置的每块骨牌没有重叠且都在边缘上，边缘上的每个位置都被已经放置的骨牌覆盖。

对于不同的子任务，作如下约定：

subtask1(5pts)：$n\le2$。

subtask2(10pts)：$n,m\le10$。

subtask3(20pts)：$n,m\le40$。

subtask4(15pts)：$n,m\le300$。

subtask5(20pts)：$n,m\le1500$。

subtask6(10pts)：$k\ge\frac{3}{2}(n+m-3)$。

subtask7(20pts)：无特殊限制。