题目背景

试题来源：https://koi.or.kr/archives/。中文翻译做了少量本土化修改。

按照署名—非商业性使用—相同方式共享 4.0 协议国际版进行授权。

题目描述

有一个由 1 到 $N$ 的 $N$ 个节点组成的树。第 $i$ 条边连接两个不同的节点 $A_i$ 和 $B_i$。（$1 \leq i \leq N - 1$）

在这 $N$ 个节点中选择一些节点，记为 $S = \{s_1, s_2, \dots, s_K\}$。如果存在 $i$ （$1 \leq i \leq K$），使得 $s_i = v$，则称节点 $v$ 属于集合 $S$。

如果集合 $S$ 中的两个不同节点 $u$ 和 $v$ 满足，仅通过集合 $S$ 中的节点即可在树上从 $u$ 移动到 $v$，则称“$u$ 和 $v$ 在 $S$ 上是连接的”。

例如，考虑如下树（$N = 7$）。如果 $K = 6$ 且 $S = \{1, 2, 3, 4, 5, 6\}$，则 “1 和 2”、“3 和 5”、“4 和 6”在集合 $S$ 上是连接的。

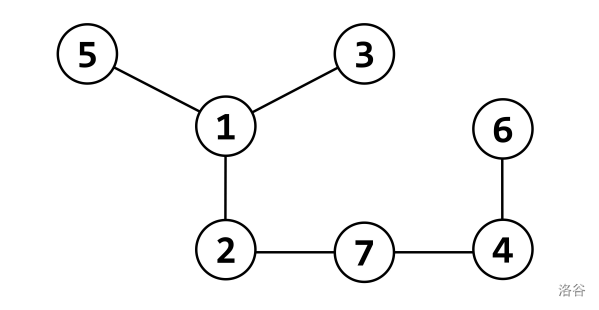
然而，“1 和 6”、“2 和 7”在集合 $S$ 上不是连接的。

我们定义满足以下条件的节点对 $(u, v)$ 的数量为集合 $S$ 的连接强度：

1. $u$ 和 $v$ 是不同的两个节点。
2. $1 \leq u < v \leq N$。
3. $u$ 和 $v$ 在集合 $S$ 上是连接的。

给定一个选择的节点集合 $S$，请计算 $S$ 的连接强度。你需要回答 $Q$ 个查询。

输入格式

第一行给出整数 $N$。

接下来 $N - 1$ 行，每行包含两个整数 $A_i$ 和 $B_i$，表示第 $i$ 条边连接的两个节点。

接着是一个整数 $Q$，表示查询的数量。

接下来 $Q$ 行，每行表示一个查询。每个查询首先给出整数 $K$，接着是 $K$ 个整数 $s_1, s_2, \dots, s_K$，表示集合 $S$。

输出格式

对于每个查询，输出一行，表示该查询中给定集合 $S$ 的连接强度。

7
1 2
1 3
1 5
2 7
4 6
4 7
6
1 1
2 1 2
4 1 2 3 4
5 1 2 4 6 7
6 1 2 3 4 5 6
7 1 2 3 4 5 6 7

0
1
3
10
7
21

提示

约束条件

• $2 \leq N \leq 250,000$
• $1 \leq Q \leq 100,000$
• 对于所有的 $i$（$1 \leq i \leq N - 1$），有 $1 \leq A_i \leq N$。
• 对于所有的 $i$（$1 \leq i \leq N - 1$），有 $1 \leq B_i \leq N$。
• 对于所有的 $i$（$1 \leq i \leq N - 1$），有 $A_i \neq B_i$。
• 给定的图是树。
• 对于每个查询，$1 \leq K \leq N$。
• 对于每个查询，给出的 K 个节点 $s_1, s_2, \dots, s_K$ 是不同的。
• 在 $Q$ 个查询中，所有的 $K$ 总和不超过 1,000,000。

子任务

1. （3 分）$N = 3$。
2. （10 分）$N \leq 50, Q \leq 50$。
3. （11 分）$N \leq 2,500, Q \leq 2,500$。
4. （13 分）每个查询中，$K = 3$。
5. （63 分）无额外约束条件。