题目描述

For a pair of points on the Cartesian plane $(x_1, y_1)$ and $(x_2, y_2)$, we define the Manhattan distance between them as $|x_1-x_2|+|y_1-y_2|$. For example, for the pair of points $(4, 1)$ and $(2, 7)$, the Manhattan distance between them is $|4-2|+|1-7| = 2+6 = 8$.

You are given $2 \cdot n$ points on the Cartesian plane, whose coordinates are integers. All $y$-coordinates of the given points are either $0$ or $1$.

Split the given points into $n$ pairs such that each of these points belongs to exactly one pair, and the maximum Manhattan distance between the points of one pair is minimized.

输入格式

The first line contains a single integer $n$ $(1 \le n \le 10^5)$.

In the following $2 \cdot n$ lines, each line contains two integers $x_i$ and $y_i$ $(0 \le x_i \le 10^9, 0 \le y_i \le 1)$ --- the coordinates of the corresponding point.

输出格式

Output a single integer --- the maximum Manhattan distance between the points of one pair in the optimal partition.

1
3 1
1 0

3

3
18 0
3 0
1 0
10 0
8 0
14 0

4

4
3 0
0 1
5 0
2 1
6 0
3 0
5 1
2 1

2

提示

In the second example, the pairing $[(18, 0), (14, 0)]$, $[(3, 0), (1, 0)]$, and $[(8, 0), (10, 0)]$ is the only optimal partition. The Manhattan distances between the points of one pair in this partition are $4$, $2$, and $2$, respectively.

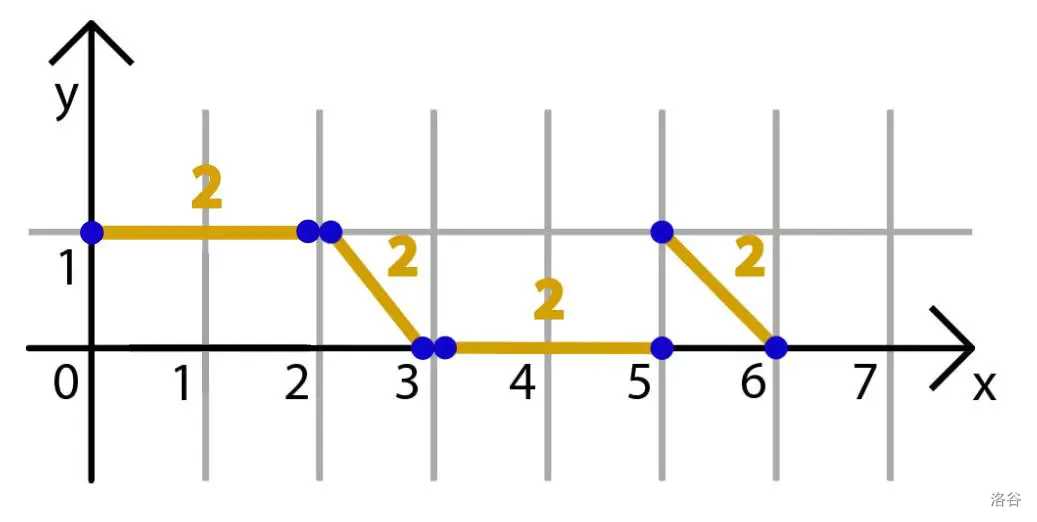
In the third example, the pairing $[(0, 1), (2, 1)]$, $[(2, 1), (3, 0)]$, $[(3, 0), (5, 0)]$, and $[(5, 1), (6, 0)]$ is an optimal partition. All Manhattan distances between the points of one pair in this partition are equal to $2$.

Illustration for the third example

Scoring

• ($2$ points): $n = 1$;
• ($3$ points): $x_i = 0$ for $1 \le i \le 2\cdot n$;
• ($4$ points): $n \le 4$;
• ($11$ points): $n \le 10$;
• ($14$ points): $y_i = 0$ for $1 \le i \le 2\cdot n$;
• ($10$ points): $x_i \neq x_j$ for $1 \le i < j \le 2\cdot n$;
• ($29$ points): $n \le 1000$;
• ($27$ points): no additional restrictions.