题目描述

给定两个集合 $S_1,S_2$，定义一个长度为 $3n$ 且仅包含 ABC 三种字符的串 $s$ 是好的，当且仅当存在一种方案将 $s$ 划分成 $n$ 个长度为 $3$ 的子序列，且这 $n$ 个子序列都是 ABC，BCA 或 CAB。设 $n$ 个子序列中 ABC 的个数为 $x$，BCA 的个数为 $y$，还要求 $x\in S_1,y\in S_2$。

现在有一个长度为 $3n$ 的字符串 $s$，字符串中仅包含 ABC? 四种字符，你需要计算将所有 ? 都分别替换成 ABC 三个字符中的某一个的方案，使得串 $s$ 是好的。

对 $2^{32}$ 取模。

输入格式

本题单个测试点内有多组测试数据

第一行两个整数 $T,id$，表示数据组数和子任务编号，保证 $T=60,id\in[0,5]$，$id=0$ 表示是样例。

对于每组数据，第一行一个整数 $n$。

第二行一个长度为 $n+1$ 的 01 串 $s_1$。若 $s_1$ 中第 $i$ 个字符为 $1$，则表示 $S_1$ 中含有 $i-1$ 这个元素，否则不含。第三行以同样的格式刻画 $S_2$。

第四行一个长度为 $3n$ 的字符串 $s$。

对于第 $i$ 组数据，保证 $n=i$。

输出格式

对于每组数据，输出一行一个整数，表示答案。

你可以选择是否回答每组数据，详情见说明部分。

3 0
1
11
11
ABC
2
101
101
A????C
3
1111
1111
?????????

1
5
1077

提示

样例解释 1

这个样例不满足 $T=60$ 的限制，仅为理解题意用。

样例 2,3

见下发文件，分别满足子任务 1,2 的性质。

提示与说明

Subtask	分值	特殊限制
1	$20$	$s$ 中没有 ?，且 $ \left\vert S_1\right\vert=\left\vert S_2\right\vert=n+1 $
2		$s$ 中没有 ?
3	$10$	$s$ 中只有 ?，且 $ \left\vert S_1\right\vert=\left\vert S_2\right\vert=n+1 $
4	$20$	$ \left\vert S_1\right\vert=\left\vert S_2\right\vert=n+1 $
5	$30$	无特殊限制

对于所有数据，保证 $T=60$。对于每个测试点内的第 $i$ 组测试数据，保证 $n=i$。

测试时开启所有合理的子任务依赖。 子任务依赖尚未配置。

对于每个测试点内的每组测试数据，如果你不打算回答这组测试数据，请输出 $-1$。否则输出一个整数表示答案。如果格式不正确不保证能得到对应的分数。

对于每个测试点，会根据你的输出给出你在这组数据上的评分系数 $p\in [0,1]$。每个 Subtask 的得分是这个 Subtask 中所有测试点得分系数的最小值乘以这个 Subtask 的分值。

首先，你的程序需要正常结束并且所有你选择回答的答案均正确，否则 $p=0$。

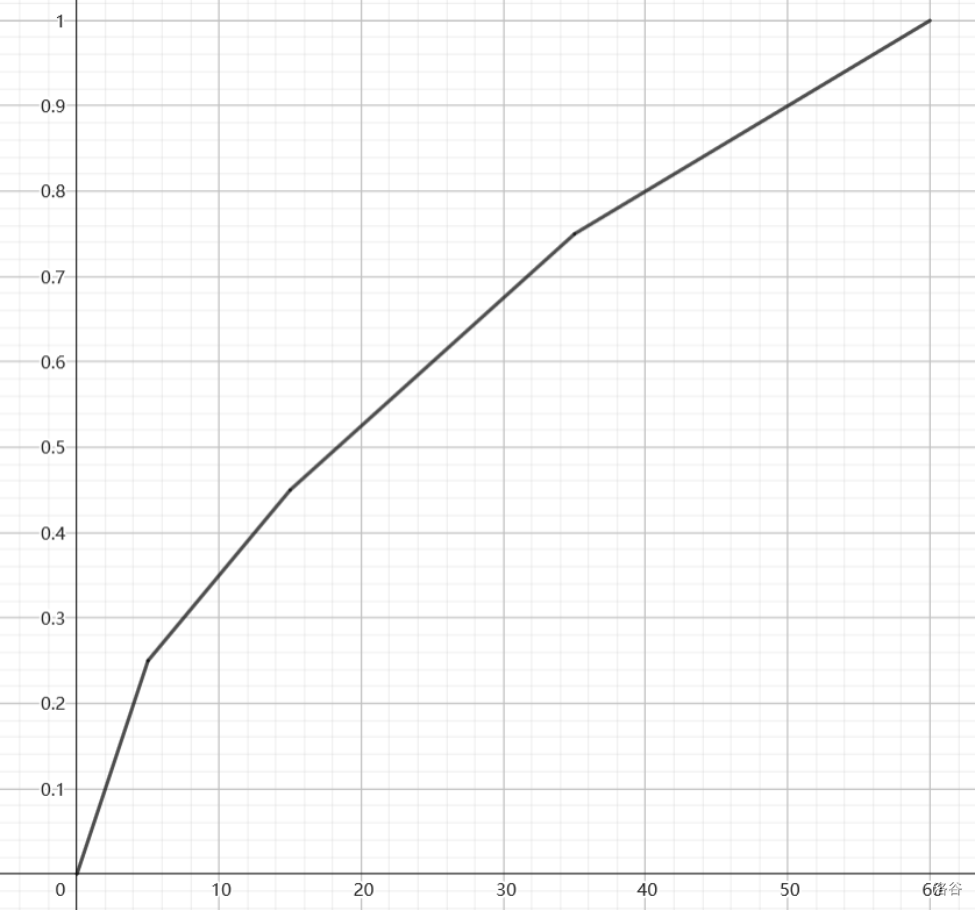
在此基础上，记 $d$ 为在所有数据中你的程序选择回答的最大的 $n$，则有

$$p= \begin{cases} \frac{1}{20} d && d\leq 5 \\ \frac{1}{4}+\frac{1}{50}(d-5) && d\leq 15 \\ \frac{9}{20}+\frac{3}{200}(d-15) && d\leq 35 \\ \frac{3}{4}+\frac{1}{100}(d-35) && d\leq 60 \end{cases} $$

$p$ 与 $d$ 的大致图像如下图所示。