题目背景

译自 COI 2025 T2。

玻利维亚坐落于南美，有着丰富的文化和自然风光。玻利维亚同时也是 IOI 2025 的举办地。

萨哈马火山（Nevado Sajama）是一个复式火山，也是玻利维亚的最高峰，位于玻利维亚奥鲁罗省和萨哈马省的交界处。

题目描述

考虑一个 $N$ 格的直方图。从左往右数第 $i$ 格的高度为 $v_i$。

这里，$N$ 是奇数，并且 $v_{(N+1)/2}$ 是 $v$ 数组的全局最大值之一。我们令 $\mathrm{mx}=v_{(N+1)/2}$。

对于整数二元组 $(A,B)$ 满足 $0\le A\lt B\le \mathrm{mx}$，我们考虑截取直方图中高度介于 $[A,B]$ 间的部分，如图所示：

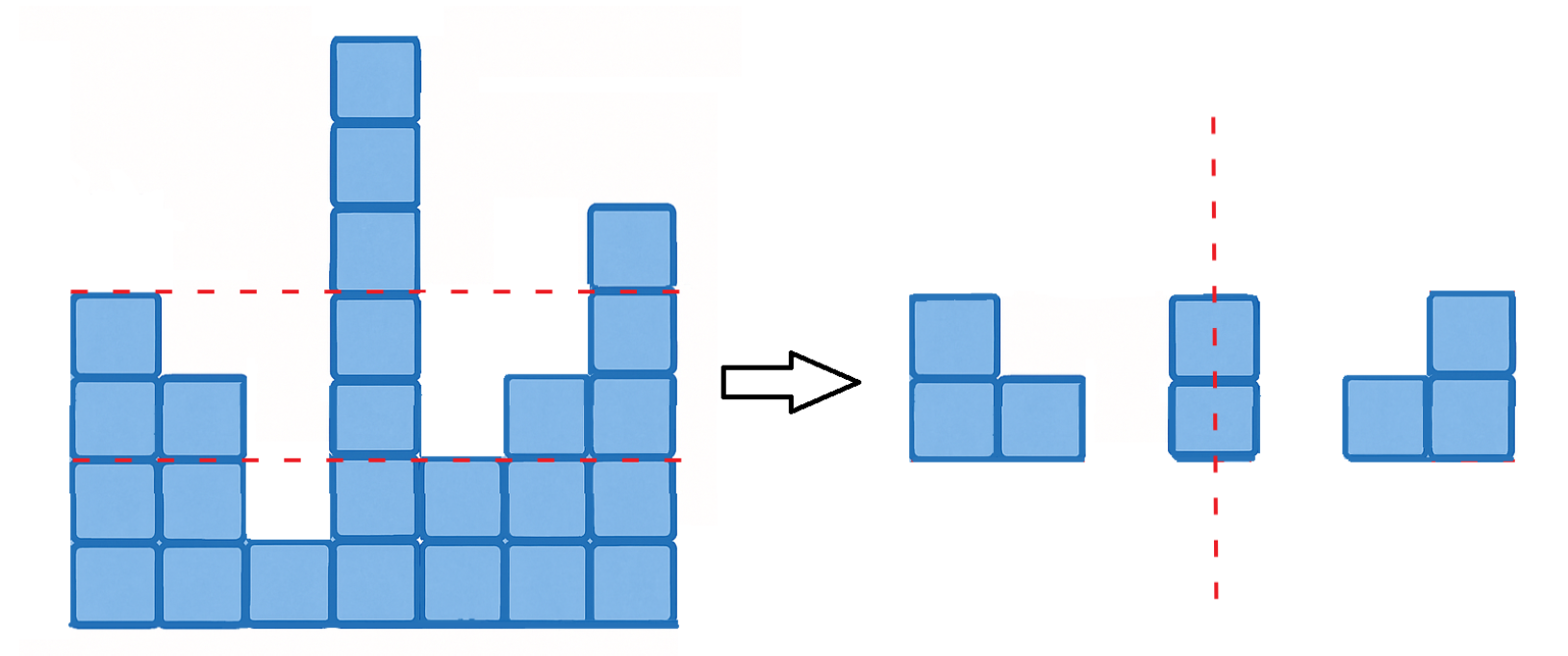
如果截取出来的部分关于位于 $(N+1)/2$ 的竖直线是对称的，我们就说 $(A,B)$ 是好的。上图就展示了一个好的 $(A,B)$，这里 $A=2,B=4$。

有 $Q$ 次对 $v$ 数组的单点修改。$\forall 1\le i\le Q+1$，求出在第 $(i-1)$ 次修改后，满足 $\forall 0\le A\lt B\le \mathrm{mx}$ 的二元组 $(A,B)$ 中，有多少个二元组是好的。

我们保证修改不会破坏「$v_{(N+1)/2}$ 是数组全局最大值之一」的性质。

输入格式

第一行，两个非负整数 $N,Q$。

第二行，$N$ 个非负整数 $v_1,v_2,\ldots,v_N$。

接下来 $Q$ 行，每行两个非负整数 $x,h$，描述一次修改 $v_{x}\gets h$。

保证 $x\neq (N+1)/2$，且 $h\le \mathrm{mx}$。

输出格式

输出 $(Q+1)$ 行，第 $i$ 仅一个非负整数，第 $(i-1)$ 次修改后的答案。

5 5
1 5 8 7 3
1 8
4 1
2 0
4 0
5 8

5
6
1
3
6
36

7 0
4 3 1 7 2 3 5

7

7 10
1 6 7 10 5 4 3
2 7
2 8
2 9
2 9
2 10
6 5
6 6
6 7
6 8
6 9

8
8
5
3
3
2
4
4
4
5
7

提示

样例解释

样例 $2$ 解释

样例 $2$ 对应的图片即为【题面描述】中的图片。

好的二元组为：$(0, 1), (2, 3), (2, 4), (3, 4), (5, 6), (5, 7), (6, 7)$，共 $7$ 个。

数据范围

• $3\le N\le 2\times 10^5$，且 $N$ 为奇数；
• $0\le Q\le 2\times 10^5$；
• $v_i\le 654\, 200$（萨哈马火山的高度为 $654200\,\mathrm{cm}$）；
• 在任意时刻，$v_{(N+1)/2}$ 是 $v$ 的一个最大值；
• $x\neq (N+1)/2$。

子任务

• $\text{Subtask 0 (0 pts)}$：样例。
• $\text{Subtask 1 (9 pts)}$：$Q=0,N\le 300,v_i\le 300$。
• $\text{Subtask 2 (23 pts)}$：$Q=0$。
• $\text{Subtask 3 (31 pts)}$：每次修改，$v_i$ 的值变化至多为 $1$。
• $\text{Subtask 4 (37 pts)}$：无额外约束。