#P10054. [CCO 2022] Phone Plans
[CCO 2022] Phone Plans
题目描述
CCOland 的市长 Jason 想要在 个住户之间安装电话线,这些住户从 到 编号。为此,他向两家竞争对手 Keenan 移动电话和 Chris 家庭电话询问了他们的电话套餐。一个公司的电话套餐对应于一个特定的等级,每条电话线都有一个等级和一个与之相关的公司。如果你从一个公司购买了等级为 的电话套餐,那么你就能够使用该公司所有等级小于或等于 的电话线。等级为 的电话套餐的价格为 ,你不能选择价格低于 的电话套餐。
两个住户只有在通过同一家公司的电话线的路径连接时才能相互通信。Jason 想要从每家公司购买一个最低成本的电话套餐,使得至少有 对不同的住户能够相互通信。
输入格式
第一行包含四个用空格分隔的整数 N, A, B 和 K,分别表示住户的数量,Keenan 移动电话的电话线的数量,Chris 家庭电话的电话线的数量,以及需要能够相互通信的最小住户对数。
接下来的 行,每行包含三个用空格分隔的整数 和 ,表示一条 Keenan 移动电话的电话线。它连接了住户 和 ,等级为 。
接下来的 行,每行包含三个用空格分隔的整数 和 ,表示一条 Chris 家庭电话的电话线,它连接了住户 和 ,等级为 。
输出格式
输出连接至少 对不同住户所需的最低成本,如果不可能,则输出 。
6 4 4 9
1 2 1
2 3 2
1 4 3
3 4 4
5 6 40
1 5 30
2 6 20
3 6 10
33
提示
样例解释
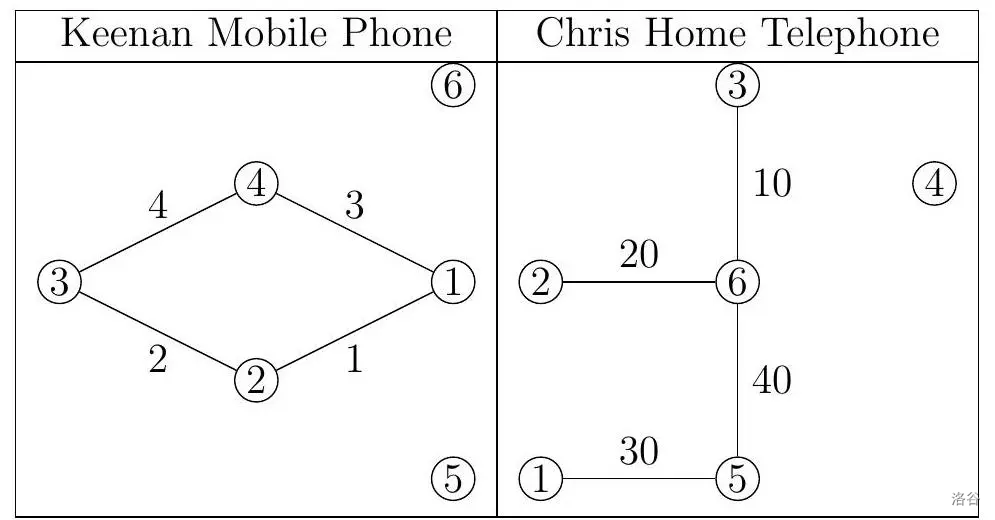
如果 Jason 从 Keenan 移动电话购买等级为 的电话套餐,从 Chris 家庭电话购买等级为 的电话套餐,那么 可以通过 Keenan 移动电话的线路相互通信,而 可以通过 Chris 家庭电话的线路相互通信。没有更便宜的方法。
数据范围
对于所有的数据,有 $1 \leq N \leq 2\times 10^5,0 \leq A, B \leq 2\times 10^5$,。
| 子任务编号 | 分值 | 附加限制 | ||
|---|---|---|---|---|
| 无 | ||||
| Keenan 移动电话只连接编号为奇数的住户;Chris 家庭电话只连接编号为偶数的住户 | ||||
| 无 | ||||
