欧拉回路

定义

• 欧拉回路：图中经过每条边恰好一次的回路
• 欧拉路径：图中经过每条边恰好一次的路径
• 欧拉图：存在欧拉回路的图
• 半欧拉图：存在欧拉路径但不存在欧拉回路的图

性质和定理

首先我们假设图是连通的，那么：

无向图的欧拉回路存在 $\Leftrightarrow$所有顶点的度为偶数。

无向图的欧拉路径存在 $\Leftrightarrow$ 只有两个顶点的度为奇数，其他顶点的度为偶数。

有向图的欧拉回路存在 $\Leftrightarrow$ 所有顶点入度=出度。

有向图的欧拉路径存在 $\Leftrightarrow$ 只有一个顶点的入度=出度+1，只有一个顶点的入度=出度-1，其他顶点的入度=出度。

算法

如何寻找欧拉回路？

1. 在图G中任意找到一个欧拉回路C并删除；
2. 在残留图中的各个极大连通子图中分别找欧拉回路并删除；
3. 将所有找到的欧拉回路合并得到最终答案。

实际实现的过程中，我们维护一个栈来存储结点，这个栈恰好可以帮我们合并回路，最后直接将栈内结点倒序输出就是答案。如果是无向图，顺序输出也可以。时间复杂度 $O(N+M)$。

# include<iostream>
using namespace std;

const int N=1e6+5,M=1e6+5;

struct edge{
	int to,next;
}e[M];

int n,cnt,top,m,t,x,y,r;
int head[N],st[N],ans[N];
bool vis[M];

void add(int x,int y){
	e[++cnt].to=y;
	e[cnt].next=head[x];
	head[x]=cnt;
}

//从指定顶点出发寻找欧拉回路 
void euler(int root){
	st[++top]=root;
	while(top){
		int x=st[top],i=head[x];
		//找尚未标记的边 
		while(i&&vis[i]) i=e[i].next;
		//沿着这条边模拟递归过程，标记该边并回溯表头 
		if(i){
			st[++top]=e[i].to;
			head[x]=e[i].next; //重新标记表头，减少循环次数 
			vis[i]=1; //如果是无向图，需要加上vis[i^1] 
		}
		//与x相邻的边均已被访问，模拟回溯过程，记录答案 
		else{
			top--;
			ans[++t]=x;
		}
	}
}

int main(){
	cin>>n>>m>>r;
	for(int i=1;i<=m;++i){
		cin>>x>>y;
		add(x,y);
		//如果是无向图，要建反边 
	}
	euler(r);
	for(int i=t;i>0;--i)
		cout<<ans[i]<<" ";
	return 0;
}

小结

欧拉回路的原理比较简单，如果能看出来一个题跟欧拉回路相关，那就很容易写出程序。因此，能不能看出这个题使用的是欧拉回路相关内容，就是解决这类问题的关键。

例题

B. 单词游戏（提高P108）

题意

将 $N$ 个仅由小写字母组成的英文单词安排一个合适的顺序，使得相邻两个单词，前一个单词的末字母等于后一个单词的首字母。请判断是否能达到这一要求。

输入：多组数据。第一行给出数据组数 $T$，每组数据第一行给出盘子数量 $N$，接下去 $N$ 行给出小写字母字符串，一种字符串可能出现多次。

输出：若存在一组合法解输出 Ordering is possible.，否则输出 The door cannot be opened.。

数据范围：$1 \le N \le 10^5, |S| \le 1000$。

解析

一个最显而易见的办法是，以单词为结点建图，如果 $i$ 能接到 $j$ 后面，就连一条 $j$ 到 $i$ 的边。那么问题就转化为了图中是否存在一条路径通过所有顶点恰好一次。这是哈密顿路径问题，难以解决。

因此我们需要重新考虑建图方法，我们可以以字母为顶点，然后以单词为边，将每个单词的首字母向它的尾字母连一条有向边。那么，我们就要找一条路径，使得这条路径通过所有边恰好一次。这是欧拉路径问题，可以解决，而且是最简单的判断是否存在欧拉路径和欧拉回路的问题，程序很简单就可以解决。

代码

# include<iostream>
# include<cstring>
# include<string>
using namespace std;

int t,n,in[30],out[30],a,b;
string s;

void solve(){
	a=b=0;
	memset(in,0,sizeof(in));
	memset(out,0,sizeof(out));
	cin>>n;
	for(int i=1;i<=n;++i){
		cin>>s;
		out[s[0]-'a']++;
		in[s[s.size()-1]-'a']++;
	}
	for(int i=0;i<26;++i){
		if(in[i]-out[i]==1) ++a;
		if(in[i]-out[i]==-1) ++b;
	}
	if(a==1&&b==1) cout<<"Ordering is possible.\n";
	else cout<<"The door cannot be opened.\n";
}

int main(){
	cin>>t;
	while(t--) solve();
	return 0;
}

D. Ant Trip（提高P110）

题意

给你简单无向图的 $N$ 个点和 $M$ 条边，问至少要几笔才能所有边都画一遍。（一笔画的时候笔不离开纸）

输入：多组数据，每组数据用空行隔开。 对于每组数据，第一行两个整数 $N,M$ 表示点数和边数。接下去 $M$ 行每行两个整数 $a,b$ 表示 $a,b$ 之间有一条边。

输出：对于每组数据，输出答案。

数据范围：$1 \le N \le 10^5, 0 \le M \le 2 \times 10^5$。

解析

直接用一个关于一笔画的结论即可：

假设图中有 $2k$ 个奇度点，则至少需要 $k$ 笔画。

代码

# include<iostream>
# include<cstring>
using namespace std;

const int N=1e5+5,M=2e5+5;
int n,m,a,b,d[N],t;

int main(){
	while(cin>>n>>m){
		t=0;
		memset(d,0,sizeof(d));
		for(int i=1;i<=m;++i){
			cin>>a>>b;
			d[a]++,d[b]++;
		}
		for(int i=1;i<=n;++i)
			if(d[i]&1) ++t;
		if(t) cout<<t/2<<endl;
		else cout<<1<<endl;
	}
	return 0;
}

E. John's Trip（提高P111）

题意

给定一个 $N$ 点 $M$ 边的无向图，问从指定点出发的欧拉回路，输出路径。

输入：多组数据，每组数据多行，每行三个整数 $x,y,z$，$z$ 为这条边的编号，$x$ 和 $y$ 为这条边的两个端点，出发点是第一条边的第一个顶点。可能有自环。每组输入数据以两个 $0$ 为结束。

输出：如果能找到路径，输出找到的路径，按顺序输出边的编号。否则输出 Round trip does not exist. 。

数据范围：$N \le 44，M \le 1995$。

解析

找欧拉回路的板子题，这题是直接输出一个欧拉回路，但是输出的是边的编号。我们在将顶点压栈的时候把对应边的编号也压进去就可以了。

F. 太鼓达人（提高P112）

题意

有 $M$ 个开关围成一圈，每个开关可能是开($1$)和关($0$)两个状态，从不同的位置出发沿顺时针检查 $K$ 个开关可以得到 $M$ 个长度为 $K$ 的 $01$ 串。现在已知这 $M$ 个 $01$ 串互不相同，以及K的值，要求最大的 $M$ 值，并且求出字典序最小的开关状态。

输入：一个整数 $K$。

输出：一行一个整数M和一个二进制串表示答案。

数据范围：$2 \le K \le 11$。

解析

这题甚至可以打表……

显然上限是 $2k$，但问题是是否能达到这个上限。

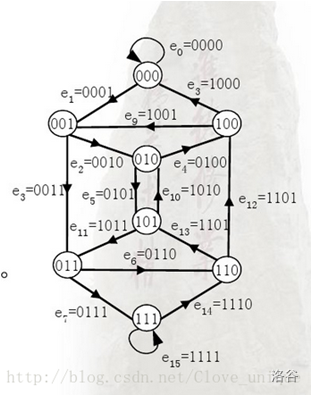
如果还是用数字作为图的顶点，$a$ 后移一位可以到 $b$ 来连边的话，又成了哈密顿路，不好。所以应该用 $k$ 位的二进制数作为边。

那问题来了，用什么作为顶点呢？应该是 $k-1$ 位二进制数。如果一条边的权值是 $x$ ，那么这条边就是从x的前缀出发，连接到 $x$ 的后缀。如图所示。

那么问题就转化为了在这个图里找欧拉回路，而且找的时候应该从最小的 $00...0$ 开始寻找，优先找后面接 $0$ 的边，这样字典序才是最小。

G. 相框（提高P113）

题意

现有一个 $N$ 个顶点 $M$ 条边的无向图，我们要把它改造成一个环，现提供以下操作：

1. 顶点分裂：把一个顶点分为若干个，原来顶点连接的边可以任意分配至新顶点处，或者不分配成为自由端。例如说，一个顶点 $x$ 连接了 $a,b,c$ 三条边，我们可以将 $x$ 复制出一个 $y$，将 $a$ 连回 $x$，$b$ 连上 $y$，$c$ 成为自由端。
2. 顶点合并：将两个自由端连接起来。

问最小操作次数。

解析

直接拆，由于环上每个点的度数是 $2$ ，因此先把度数大于 $2$ 的顶点拆开，如果有零头，留一个度数为 $1$ 的顶点。

由欧拉路径的结论可知，按这个拆法，一个有 $k$ 个奇度点的连通块存在一种方案可以拆成 $\frac k 2$ 条链，一个全是偶度点的连通块可以直接拆成一个环。

然后如果有不止一个连通块，拆掉所有环。

最后把所有链拼起来成环。

利用上述结论统计次数即可。

H. 原始生物（提高P114）

建图很直接，将限制建边即可。于是题目就变成了在每个连通块里找一些欧拉路径然后将它们用最短的方法来连接。

如果一个连通块本身是欧拉路径，那么这个连通块不需要加边。

否则，假设有 $2k$ 个奇点，那么根据定理，可以找到 $k$ 条欧拉路径。那就是找 $2k-2$ 个点，在这些点之间连边，使得边数最小。

本质上就是加最少的边使得整个图可以分解成若干欧拉回路。

练习

P1341 无序字母对

# include<iostream>
using namespace std;

const int N=55,M=1500;
int n=52,m,x,y,t;
int fa[N],f=-1;
int d[N],s=1;
int g[N][N];
int k,ans[M];
char a,b;

int ctoi(char c){
	if(c<='Z') return c-'A'+1;
	else return c-'a'+27;
}

char itoc(int x){
	if(x<=26) return x-1+'A';
	else return x-27+'a';
}

int find(int x){
	if(fa[x]==x) return x;
	else return fa[x]=find(fa[x]);
}

void merge(int x,int y){
	int p=find(x),q=find(y);
	if(p!=q) fa[p]=fa[x]=fa[y]=q;
}

bool check(){
	for(int i=1;i<=n;++i)
		if(d[i]){
			f=find(i);
			break;
		}
	for(int i=1;i<=n;++i){
		if(d[i]&&find(i)!=f) return 0;
		if(d[i]&1) t++;
	}
	if(t>2) return 0;
	else return 1;
}

void euler(int u){
	for(int i=1;i<=n;++i)
		if(g[u][i]>=1){
			g[u][i]--,g[i][u]--;
			euler(i);
		}
	ans[++k]=u;
}

int main(){
	cin>>m;
	for(int i=1;i<=n;++i) fa[i]=i;
	for(int i=1;i<=m;++i){
		cin>>a>>b;
		x=ctoi(a),y=ctoi(b);
		g[x][y]++,g[y][x]++;
		d[x]++,d[y]++;
		merge(x,y);
	}
	if(check()){
		while(!d[s]) s++;
		for(int i=1;i<=n;++i)
			if(d[i]&1){
				s=i;
				break;
			}
		euler(s);
		for(int i=k;i>=1;--i)
			cout<<itoc(ans[i]);
	}
	else cout<<"No Solution";
	return 0;
}

P2731 骑马修栅栏

# include<iostream>
using namespace std;

const int N=505,M=1030;
int n=500,m,x,y,s=1;
int d[N];
int k,ans[M];
int g[N][N];

void euler(int u){
	for(int i=1;i<=n;++i)
		if(g[u][i]>=1){
			g[u][i]--;
			g[i][u]--;
			euler(i);
		}
	ans[++k]=u;
}

int main(){
	cin>>m;
	for(int i=1;i<=m;++i){
		cin>>x>>y;
		g[x][y]++,g[y][x]++;
		d[x]++,d[y]++;
	}
	for(int i=1;i<=n;++i)
		if(d[i]&1){
			s=i;
			break;
		}
	euler(s);
	for(int i=k;i>=1;--i)
		cout<<ans[i]<<endl;
	return 0;
}

P7771 【模板】欧拉路径（半成品）

# include<iostream>
# include<vector>
# include<algorithm> 
using namespace std;

const int N=1e5+5,M=2e5+5;
int n,m,x,y,cnt;
int in[N],out[N],s=1;
int k,ans[N];
bool vis[M];

struct edge{
	int v,id;
	edge(int _v,int _id){
		v=_v,id=_id;
	}
};
vector<edge> e[N];

void add(int x,int y){
	e[x].push_back(edge(y,++cnt));
	in[y]++,out[x]++;
}

bool cmp(edge x,edge y){
	return x.v>y.v;
}

bool check(){
	int n1=0,n2=0;//入<出，入>出 
	for(int i=1;i<=n;++i){
		if(in[i]==out[i]-1) ++n1,s=i;
		if(in[i]==out[i]+1) ++n2;
		if(n1>1||n2>1) return 0;
	}
	return 1;
}

void euler(int u){
	int i=e[u].size()-1;
	while(i>=0){
		while(i>=0&&vis[e[u][i--].id])
			e[u].pop_back();
		if(i<0) return;
		vis[e[u][i].id]=1;
		euler(e[u][i].v);
		ans[++k]=u;
		i=e[u].size()-1;
	}
}

int main(){
	cin>>n>>m;
	for(int i=1;i<=m;++i){
		cin>>x>>y;
		add(x,y);
	}
	if(!check()){
		cout<<"No";
		return 0;
	}
	for(int i=1;i<=n;++i)
		sort(e[i].begin(),e[i].end(),cmp);
	euler(s);
	cout<<k;
	for(int i=k;i>=1;--i)
		cout<<ans[i]<<" ";
	return 0;
}

作业

提高域

洛谷域