「EZEC-2」甜梦
You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.
题目背景
昨是今非望无尽,生死相隔两茫茫。
解愁肠,度思量,人间如梦,倚笑乘风凉。
题目描述
有 个梦境场景,编号 且互不相同。PF 有精神分裂症,他在同一时间会处于两个梦境。这两个梦境所在的场景编号差别的绝对值不能大于 。场景之间有 种单向关系,其中第 个关系连接场景 和 。不存在不可能到达的场景。
每个场景都有一个快乐值,其中第 个场景的快乐值为 ,在梦境第一次经过时增加。
一开始两个梦境均在场景 ,当两个梦境都移动到场景 时,PF会醒来。
如果某次移动时,PF 目前梦境所在的两个场景 都与某个场景 直接相连,那么 PF 可以同时移动 两个梦境到达场景 。否则,PF 一次只能移动一个梦境。
请你编一个程序,来计算醒来时可能得到的最大快乐值。
输入格式
第一行三个整数 ,分别表示场景的数量,场景之间的关系数量,以及 PF 两个场景距离的最大值。
接下来一行 个整数,第 个数表示编号为 的场景的快乐值为 ,场景 和场景 的快乐值为 。
接下来 行,每行两个整数 ,表示场景之间存在的一条单向关系。
输出格式
如果有解,一行一个整数 ,表示能获得的最大快乐值。
如果无解,只需输出 -1。
7 9 2
0 4 5 10 10 20 0
1 2
1 3
1 4
1 6
2 5
3 5
4 7
5 7
6 7
25
提示
【样例解释 #1】
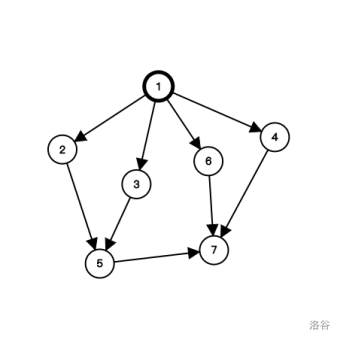
下文用 表示目前正在进行的梦境:
移动梦境 ,移动梦境 ,移动梦境 ,之后同时移动梦境 到达场景 ,快乐值总和为 。
注意:如果想移动某一梦境到场景 ,那么另一梦境的编号必须大于等于 。然而到 的线路只有 ,而同时拥有场景 和场景 不满足中间相隔场景 ,故唯一通过场景 的方案为将两个梦境同时移动到场景 ,而这么做能得到的快乐值为 。
【数据范围与约定】
| 测试点编号 | 时间 | 特殊性质 | ||||
|---|---|---|---|---|---|---|
| 无 | ||||||
| 场景是一棵树 | ||||||
| 无 | ||||||
对于 的数据,, , , , 。
输入保证每个场景都能从起点到达,并且都能连到终点。
输入不保证没有重边。
输入不对 的编号差做任何保证。
【移动范例】
假设 且关系存在,下面的格式表示 一次移动:
- (√)
- (×)
- (√)
- (×)
20241217集训
- Status
- Done
- Rule
- IOI
- Problem
- 5
- Start at
- 2024-12-17 17:00
- End at
- 2024-12-17 21:30
- Duration
- 4.5 hour(s)
- Host
- Partic.
- 13
