[COCI2009-2010#4] OGRADA
You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.
题目描述
译自 COCI 2010.02 T4「OGRADA」
Matija 的栅栏由 条木板组成,从左到右依次编号为 。 号木板的高度为 ,每条木板的宽度是 。
Matija 想用一个宽度为 的滚筒刷来刷木板。使用滚筒刷时,要保证刷子完全接触栅栏(不能一部分接触一部分不接触);另外,还要保证滚筒平行于地面。因此,每次涂色时,Matija 会在栅栏上选择连续的 条木板,然后从下往上「刷」,一直刷到这 条木板中最矮者的高度。
根据上述规则,有可能有一些木板没法用滚筒刷来刷,Matija 不得不用牙刷来「涂」剩下的部分。因此,请帮他求出他最少只需用牙刷「涂」多少平方厘米。他还想知道,在满足「涂」的面积最少的情况下,他最少要用滚筒刷「刷」多少次。
输入格式
第一行:。
第二行:。
输出格式
两行。
第一行有一个整数,表示 Matija 最少需用牙刷涂多少平方厘米。
第二行有一个整数,表示最少要用滚筒刷「刷」多少次。
5 3
5 3 4 4 5
3
2
10 3
3 3 3 3 3 3 3 3 3 3
0
4
7 4
1 2 3 4 3 2 1
4
4
提示
样例说明 1
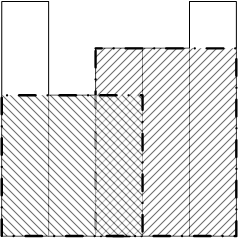
数据范围与提示
.
国庆提高组30题(1~3号)
- Status
- Done
- Rule
- IOI
- Problem
- 28
- Start at
- 2024-9-29 17:00
- End at
- 2024-10-8 1:00
- Duration
- 200 hour(s)
- Host
- Partic.
- 55
