#P9885. [ICPC 2018 Qingdao R] Sequence and Sequence
[ICPC 2018 Qingdao R] Sequence and Sequence
题目描述
Consider the following two sequences and . We denote as the -th element in sequence , and as the -th element in sequence :
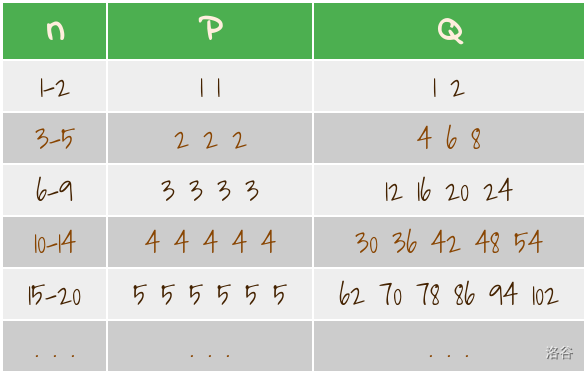
- Sequence is a sequence where for all , appears in sequence for times ( is the set of all positive integers). That is to say, $P = \{1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, \dots \}$
- Sequence can be derived from the following equations:
That is to say, $Q = \{1, 2, 4, 6, 8, 12, 16, 20, 24, 30, 36, 42, 48, 54, 62, \dots \}$
Given a positive integer , please calculate the value of .
输入格式
There are multiple test cases. The first line of the input contains an integer (about ), indicating the number of test cases. For each test case:
The first and only line contains an integer ().
输出格式
For each test case output one line containing one integer, indicating the value of .
4
10
100
1000
987654321123456789
30
2522
244274
235139898689017607381017686096176798
