#P9875. [EC Final 2021] Two Walls
[EC Final 2021] Two Walls
题目描述
Prof. Pang has bought a humanoid cleaning robot to clean his yard. The robot is not very sophisticated. It can either move forward or change its direction at a time, all controlled by Prof. Pang's controller.
Prof. Pang's yard is a 2D plane. The robot needs to move from its current location to the destination to fulfill some cleaning needs of Prof. Pang. However, there are two straight walls and in Prof. Pang's yard. Since the robot is clumsy, it will fall over if it touches any of the walls (even at endpoints).
Now that Prof. Pang is lazy, he wants to minimize the number of times the robot changes its direction. Can you help him?
输入格式
The first line contains a single integer () denoting the number of test cases.
For each test case, the first line contains two integers , the coordinates of point . The second line contains two integers , the coordinates of point . The third line contains four integers , the coordinates of point and which are the endpoints of the first wall. The fourth line contains four integers , the coordinates of point and which are the endpoints of the second wall.
It is guaranteed that neither the current location nor the destination of the robot are on any of the walls. A wall may degenerate to a point. It can be proved that the robot can always move from to without touching any of the walls. All values lie within .
输出格式
For each test case, print one number in one line, denoting the minimum number of turns.
题目大意
平面直角坐标系上有两点 与 ,以及两面墙 ,墙可以视作线段。
请问从 到 在不碰到墙(端点也不可碰到)的情况下最少要转几次弯(转弯的度数可以任意决定)?
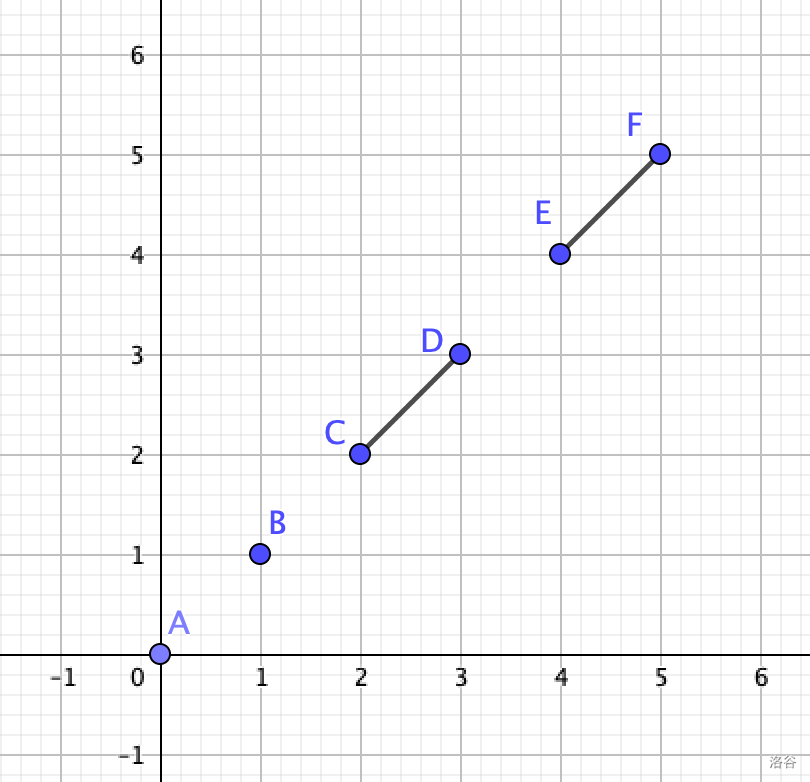
3
0 0
1 1
2 2 3 3
4 4 5 5
0 0
1 1
2 2 3 3
2 2 3 3
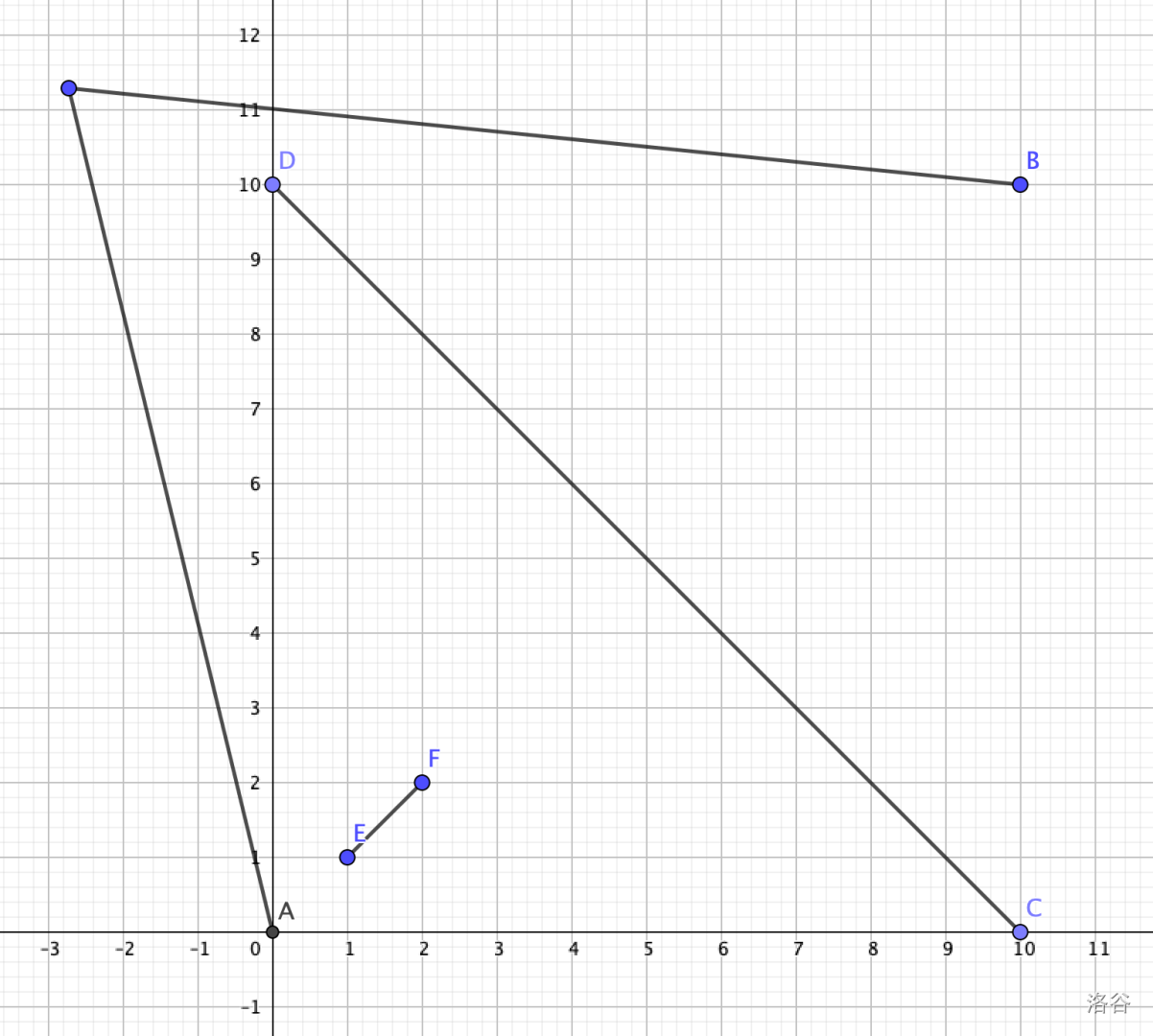
0 0
10 10
10 0 0 10
1 1 2 2
0
0
1
提示
The following are illustrations for the first sample and the third sample.