#P9827. [ICPC 2020 Shanghai R] Sky Garden
[ICPC 2020 Shanghai R] Sky Garden
题目描述
Prof. Du and Prof. Pang plan to build a sky garden near the city of Allin. In the garden, there will be a plant maze consisting of straight and circular roads.
On the blueprint of the plant maze, Prof. Du draws circles indicating the circular roads. All of them have center . The radius of the -th circle is .
Meanwhile, Prof. Pang draws lines on the blueprint indicating the straight roads. All of the lines pass through . Each circle is divided into parts with equal lengths by these lines.
Let be the set of the roads. Let be the set of all intersections of two different roads in . Note that each circular road and each straight road have two intersections.
For two different points and , we define to be the shortest distance one needs to walk from to along the roads. Please calculate the sum of for all .
输入格式
The only line contains two integers .
输出格式
Output one number -- the sum of the distances between every pair of points in .
Your answer is considered correct if its absolute or relative error does not exceed .
1 2
14.2831853072
2 3
175.4159265359
提示
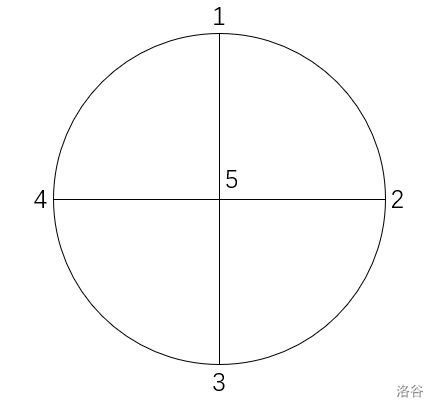
$dis(p_1, p_2)=dis(p_2, p_3)=dis(p_3, p_4)=dis(p_1, p_4)=\frac{\pi}{2}$
$dis(p_1, p_5)=dis(p_2, p_5)=dis(p_3, p_5)=dis(p_4, p_5)=1$
