题目背景

一点也不美丽的不死鸟。

那双锐爪，沾染了无辜的鲜血。

题目描述

给定二元序列 $\{(v_i,c_i)\}$ 和一棵以 $1$ 为根的有根树。第 $i$ 个点的点权是 $(v_i,c_i)$。

• 定义一个非根节点的权值为其子树内的 $c$ 的积乘上其子树补的 $v$ 的积。
• 定义一个根节点的权值为其子树内的 $c$ 的积。

形式化的讲，若 $u$ 不为根节点，则 $u$ 的权值 $f_u$ 为：

$$f_u=\prod\limits_{v\in \operatorname{substree}(u)} c_v\times \prod\limits_{v\notin \operatorname{substree}(u)} v_v $$

否则，其权值 $f_u$ 为：

$$f_u=\prod\limits_{v=1}^n c_v$$

试求整棵树所有节点的权值之和，答案对 $m$ 取模。请注意：保证 $\bm m$ 是质数。

输入格式

第一行两个正整数 $n,m$。

接下来 $n-1$ 行，每行两个数 $u,v$，表示 $u,v$ 之间有一条边。

接下来一行 $n$ 个数，表示 $c_{1, 2, \dots, n}$。

接下来一行 $n$ 个数，表示 $v_{1, 2, \dots, n}$。

输出格式

输出一个数，表示答案对 $m$ 取模后的结果。

3 998244853
1 2
1 3
2 1 2
1 2 2

10

5 998244353
1 2
1 3
1 4
4 5
5 5 5 2 3
6 6 1 5 3

4656

提示

样例解释

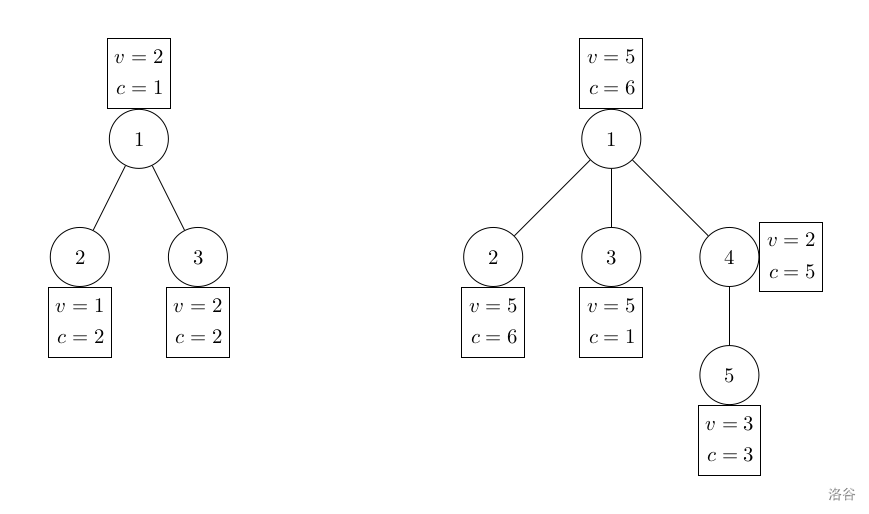
（图片有误，应该交换 $v,c$ 的权值。）

数据范围及约定

对于 $100\%$ 的数据，满足 $1\le n\leq 3\times 10^5$，$1\leq v_i,c_i,m\leq 10^9$。