题目描述

在这一轮的星际战争中，我方在宇宙中建立了 $n$ 个据点，以 $m$ 个单向虫洞连接。我们把终点为据点 $u$ 的所有虫洞归为据点 $u$ 的虫洞。

战火纷飞之中这些虫洞很难长久存在，敌人的打击随时可能到来。这些打击中的有效打击可以分为两类：

1. 敌人会摧毁某个虫洞，这会使它连接的两个据点无法再通过这个虫洞直接到达，但这样的打击无法摧毁它连接的两个据点。
2. 敌人会摧毁某个据点，由于虫洞的主要技术集中在出口处，这会导致该据点的所有还未被摧毁的虫洞被一同摧毁。而从这个据点出发的虫洞则不会摧毁。

注意：摧毁只会导致虫洞不可用，而不会消除它的存在。

为了抗击敌人并维护各部队和各据点之间的联系，我方发展出了两种特种部队负责修复虫洞：

• A 型特种部队则可以将某个特定的虫洞修复。
• B 型特种部队可以将某据点的所有损坏的虫洞修复。

考虑到敌人打击的特点，我方并未在据点上储备过多的战略物资。因此只要这个据点的某一条虫洞被修复，处于可用状态，那么这个据点也是可用的。

我方掌握了一种苛刻的空间特性，利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营，实现精确打击。

为了把握发动反攻的最佳时机，指挥部必须关注战场上的所有变化，为了寻找一个能够进行反攻的时刻。总指挥认为：

• 如果从我方的任何据点出发，在选择了合适的路线的前提下，可以进行无限次的虫洞穿梭（可以多次经过同一据点或同一虫洞），那么这个据点就可以实现反击。
• 为了使虫洞穿梭的过程连续，尽量减少战舰在据点切换虫洞时的质能损耗，当且仅当只有一个从该据点出发的虫洞可用时，这个据点可以实现连续穿梭。
• 如果我方所有据点都可以实现反击，也都可以实现连续穿梭，那么这个时刻就是一个绝佳的反攻时刻。

总司令为你下达命令，要求你根据战场上实时反馈的信息，迅速告诉他当前的时刻是否能够进行一次反攻。

输入格式

输入的第一行包含两个正整数 $n,m$。

接下来 $m$ 行每行两个数 $u,v$，表示一个从据点 $u$ 出发到据点 $v$ 的虫洞。保证 $u \ne v$，保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。

接下来一行一个正整数 $q$ 表示询问个数。

接下来 $q$ 行每行表示一次询问或操作。首先读入一个正整数 $t$ 表示指令类型：

• 若 $t = 1$，接下来两个整数 $u, v$ 表示敌人摧毁了从据点 $u$ 出发到据点 $v$ 的虫洞。保证该虫洞存在且未被摧毁。
• 若 $t = 2$，接下来一个整数 $u$ 表示敌人摧毁了据点 $u$。如果该据点的虫洞已全部被摧毁，那么这次袭击不会有任何效果。
• 若 $t = 3$，接下来两个整数 $u, v$ 表示我方修复了从据点 $u$ 出发到据点 $v$ 的虫洞。保证该虫洞存在且被摧毁。
• 若 $t = 4$，接下来一个整数 $u$ 表示我方修复了据点 $u$。如果该据点没有被摧毁的虫洞，那么这次修复不会有任何效果。

在每次指令执行之后，你需要判断能否进行一次反攻。如果能则输出 YES 否则输出 NO。

输出格式

输出一共 $q$ 行。对于每个指令，输出这个指令执行后能否进行反攻。

3 6
2 3
2 1
1 2
1 3
3 1
3 2
11
1 3 2
1 2 3
1 1 3
1 1 2
3 1 3
3 3 2
2 3
1 3 1
3 1 3
4 2
1 3 2

NO
NO
YES
NO
YES
NO
NO
NO
YES
NO
NO

提示

【样例解释 #1】

虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞：

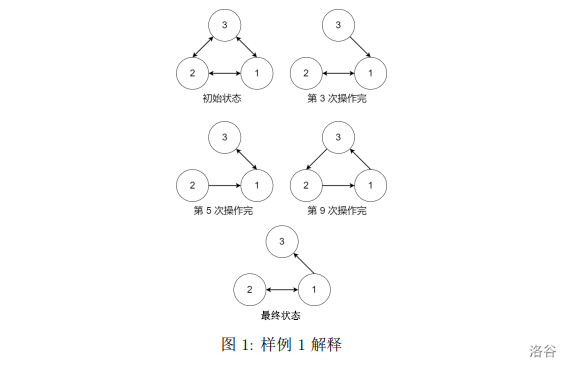
【样例 #2】

见附件中的 galaxy/galaxy2.in 与 galaxy/galaxy2.ans。

【样例 #3】

见附件中的 galaxy/galaxy3.in 与 galaxy/galaxy3.ans。

【样例 #4】

见附件中的 galaxy/galaxy4.in 与 galaxy/galaxy4.ans。

【数据范围】

对于所有数据保证：$1 \le n \le 5 \times {10}^5$，$1 \le m \le 5 \times {10}^5$，$1 \le q \le 5 \times {10}^5$。

测试点	$n \le$	$m \le$	$q \le$	特殊限制
$1 \sim 3$	$10$	$20$	$50$	无
$4 \sim 8$	${10}^3$	${10}^4$	${10}^3$
$9 \sim 10$	$5 \times {10}^5$	$5 \times {10}^5$	$5 \times {10}^5$	保证没有 $t = 2$ 和 $t = 4$ 的情况
$11 \sim 12$				保证没有 $t = 4$ 的情况
$13 \sim 16$	${10}^5$			无
$17 \sim 20$	$5 \times {10}^5$	$5\times 10^5$