题目描述

定义由若干个边长为 $1$ 的正方体方块搭成的立体图形的「侧面积」为：对于所有方块，若它的前、后、左或右面没有紧贴着另一个方块，则该面计入侧面积。

维护长宽均无限的矩形地面，地面被划分为若干个边长为 $1$ 的格子。$n$ 次操作，每次选择一个格子 $(x_i,y_i)$ 在该位置向上堆叠 $z_i$ 个边长为 $1$ 的正方体方块。每次操作后，输出整个立体图形的「侧面积」。

输入格式

• 第一行输入一个整数 $n$。
• 接下来 $n$ 行，每行输入三个整数 $x_i,y_i,z_i$。

输出格式

• 输出共 $n$ 行，每行输出一个整数。表示每次操作后立体图形的「侧面积」。

3
1 1 2
1 3 3
1 2 4

8
20
26

6
1 2 1
2 1 4
2 3 8
3 2 6
2 2 2
2 2 11

4
20
52
76
70
90

提示

样例 1 解释

如图所示，建立空间直角坐标系。注意这里的空间直角坐标系和数学上常用的略有区别，其 $x$-轴向南、$y$-轴向东、$z$-轴向上。限于技术原因，此处仅给出斜二测画法的立体图形，请读者自行脑补立体图形其他角度的模样。图中绿色部分即为立体图形的侧面。

第一次操作后，在 $(1,1)$ 位置放入了一个高度为 $2$ 的立体图形，侧面积为 $8$。

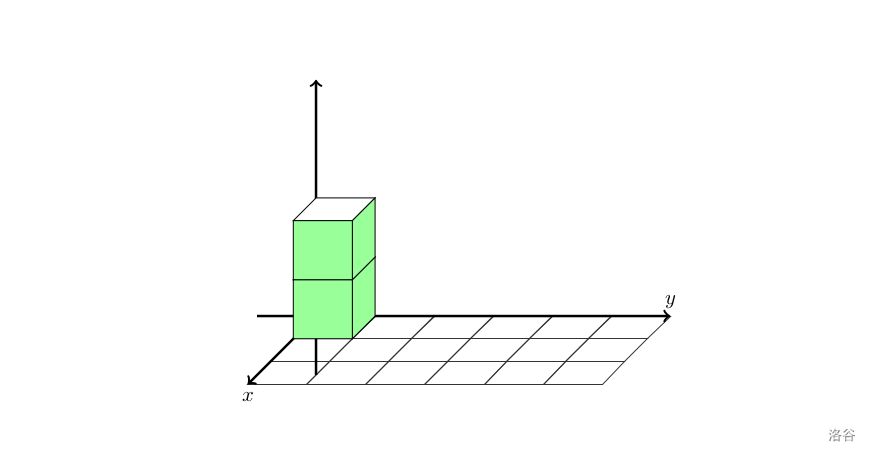
第二次操作后，在 $(1,3)$ 位置放入了一个高度为 $3$ 的立体图形，侧面积为 $12$。由于两个立体图形没有接触，因此可以直接加上第一次放上的立体图形的侧面积，总侧面积为 $20$。

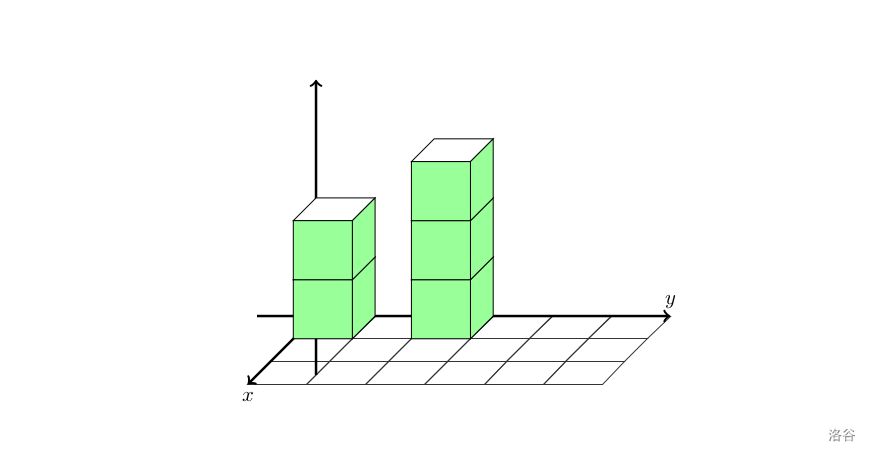
第三次操作后，在 $(1,2)$ 位置放入了一个高度为 $4$ 的立体图形。由于某些面发生了接触，这些面对应的面积不计入侧面积的计算范围内。容易发现，总侧面积为 $26$。

---

再强调下，每次堆叠操作是在对应位置上再加上 $z_i$ 个方块。例如下图，是先执行了 $\verb!2 2 1!$，再执行了 $\verb!2 2 3!$ 的结果。

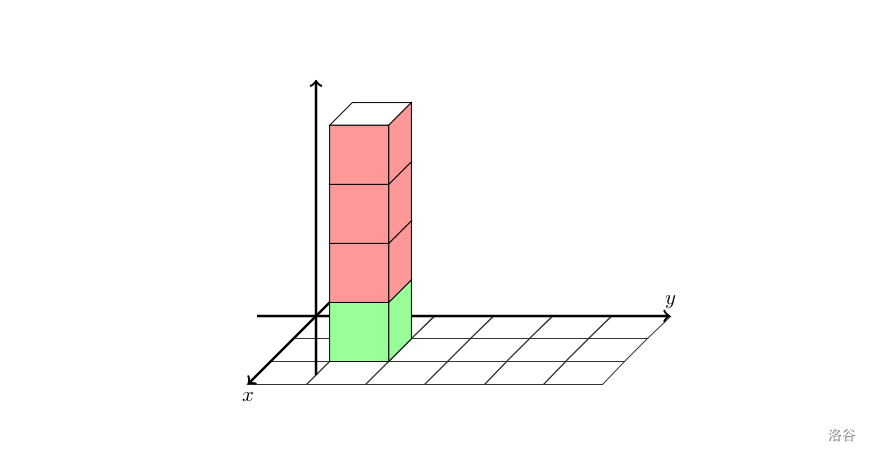
附加样例

• 样例 $3$ 见下发文件中的 $\textbf{\textit{two3.in/two3.ans}}$。该样例满足测试点 $4$ 的限制。
• 样例 $4$ 见下发文件中的 $\textbf{\textit{two4.in/two4.ans}}$。该样例满足测试点 $7$ 的限制。
• 样例 $5$ 见下发文件中的 $\textbf{\textit{two5.in/two5.ans}}$。该样例满足测试点 $10$ 的限制。
• 样例 $6$ 见下发文件中的 $\textbf{\textit{two6.in/two6.ans}}$。该样例满足测试点 $13$ 的限制。
• 样例 $7$ 见下发文件中的 $\textbf{\textit{two7.in/two7.ans}}$。该样例满足测试点 $20$ 的限制。

数据范围

$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|c||c|c|c|c|c|} \hline \textbf{\textsf{\#}} & \bm{{n \le }} & \bm{{x,y \le}} & \bm{{z \le}} & \textbf{\textsf{特殊性质}} & \textbf{\textsf{\#}} & \bm{{n \le }} & \bm{{x,y \le}} & \bm{{z \le}} & \textbf{\textsf{特殊性质}} \cr\hline 1 & 1 & 1 & 10 & - & 14 & 10^3 & 10^3 & 10^3 & - \cr\hline 2 & 2 & 5 & 10 & - & 15 & 10^3 & 10^3 & 10^9 & - \cr\hline 3 & 10 & 5 & 10 & - & 16 & 10^3 & 10^9 & 10^9 & - \cr\hline 4 & 100 & 100 & 100 & - & 17 & 10^5 & 10^9 & 10^9 & \textbf{AB} \cr\hline 5 & 10^3 & 10^3 & 10^3 & \textbf{AB} & 18 & 10^5 & 10^9 & 10^9 & \textbf{A} \cr\hline 6 & 10^3 & 10^3 & 10^9 & \textbf{AB} & 19 & 10^5 & 10^9 & 10^9 & \textbf{B} \cr\hline 7 & 10^3 & 10^9 & 10^9 & \textbf{AB} & 20 & 10^5 & 10^9 & 10^9 & - \cr\hline 8 & 10^3 & 10^3 & 10^3 & \textbf{A} & 21 & 2\times 10^5 & 10^9 & 10^9 & - \cr\hline 9 & 10^3 & 10^3 & 10^9 & \textbf{A} & 22 & 2\times 10^5 & 10^9 & 10^{12} & - \cr\hline 10 & 10^3 & 10^9 & 10^9 & \textbf{A} & 23 & 2\times 10^5 & 10^9 & 10^{13} & \textbf{A} \cr\hline 11 & 10^3 & 10^3 & 10^3 & \textbf{B} & 24 & 2\times 10^5 & 10^9 & 10^{13} & - \cr\hline 12 & 10^3 & 10^3 & 10^9 & \textbf{B} & 25 & 3\times 10^5 & 10^9 & 10^{13} & - \cr\hline 13 & 10^3 & 10^9 & 10^9 & \textbf{B} &&&&&\cr\hline \end{array} $$

• 特殊限制 $\bf A$：$\forall 1 \le i\le j \le n$，有 $x_i=x_j$。
• 特殊限制 $\bf B$：$\forall 1 \le i\le j \le n$，有 $(x_i,y_i) \ne (x_j,y_j)$。

对于 $100\%$ 的数据，保证 $1 \le n \le 3 \times 10^5$，$1 \le x,y \le 10^9$，$1\le z \le 10^{13}$。