题目背景

本题只支持 C++ 提交，提交时不需要包含 mars.h 头文件，只需要将附件中的 mars.h 中的内容粘贴到代码的开头即可。

请使用 C++14、C++17 等语言，而不是 C++14 (GCC 9)，因为一些未知原因这个语言下 SPJ 会 CE。

【注】：洛谷暂不支持题面中所说的评测方式，我实现了一个洛谷支持的简易版本的交互库，但不能对传递数据进行有效限制，请各位自觉。

题目描述

你们晓得，法老们是最先去过外太空的人。他们发射过首次登陆行星图特摩斯一世（Thutmus I，现在一般叫它火星）的飞船。行星的表面可以建模成由方形单元构成的 $(2n + 1) \times (2n + 1)$ 网格，其中每个单元中或者为陆地、或者为水域。对于第 $i$ 行第 $j$ 列（$0 \le i, j \le 2 \cdot n$）的单元，如果单元中为陆地，则其状态表示为 $s[i][j] = \texttt{1}$；如果单元中为水域，则表示为 $s[i][j] = \texttt{0}$。

如果在两个陆地单元之间存在某条仅由陆地单元构成的路径，而且路径中每两个连续的前后单元都有公共边，则称这两个陆地单元是连通的。行星上的岛屿被定义为两两连通的陆地单元的极大集合。

飞船的任务是统计该行星上岛屿的数量。然而，考虑到飞船的上古电脑，这事儿并不容易。电脑的内存储器 $h$ 以一个 $(2n + 1) \times (2n + 1)$ 的二维数组的形式存储数据，且数组的每个位置上可以保存长度为 $100$ 的字符串，串中的每个字母为 $\texttt{0}$（ASCII 码 $48$）或 $\texttt{1}$（ASCII 码 $49$）。初始时，存储器的每个位置的第 $0$ 位记录的是上述网格中每个单元的状态，即 $h[i][j][0] = s[i][j]$（对所有 $0 \le i, j \le 2 \cdot n$）。$h$ 中的其他位在初始时都被置为 $\texttt{0}$（ASCII 码 $48$）。

在处理存储器中的数据时，电脑只能访问存储器中的 $3 \times 3$ 区块，并且改写该区块左上角位置的值。说得更正式一点，电脑可以访问 $h[i \dots i + 2][j \dots j + 2]$（$0 \le i, j \le 2 \cdot (n - 1)$）中的值，并且改写 $h[i][j]$ 中的值。在 下文中，该过程被叫做处理单元 $(i, j)$。

为了解决电脑能力的局限，法老们搞出了下面的套路：

• 电脑可以分成 $n$ 个阶段来操作存储器。
• 在阶段 $k$（$0 \le k \le n - 1$），令 $m = 2 \cdot (n - k - 1)$， 电脑将对所有的 $0 \le i, j \le m$，按照 $i$ 的升序以及每个 $i$ 上 $j$ 的升序，处理单元 $(i, j)$。换句话说，电脑将按照如下顺序处理这些单元：$(0, 0), (0, 1),\cdots , (0, m), (1, 0), (1, 1),\cdots , (1, m),\cdots , (m, 0), (m, 1),\cdots , (m, m)$。
• 在最后一个阶段（$k = n - 1$），电脑仅处理单元 $(0, 0)$。该阶段结束后，写入到 $h[0][0]$ 的值应该等于行星上的岛屿数量，而且该值应以字符串的形式表示成二进制，其中最低有效位对应于字符串的首字符。

下图给出了电脑操作某个 $5 \times 5$（$n = 2$）存储器的方式。蓝色单元表示该单元正在被改写，而着色的单元则表示被处理的子数组。

在阶段 $0$，电脑将以如下顺序处理下面的子数组：

在阶段 $1$，电脑将仅处理一个子数组：

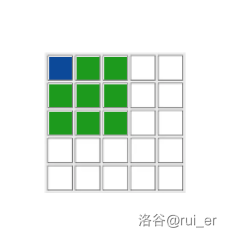
你的任务是给出一个方法，让电脑能在给定的操作方式下，统计出行星图特摩斯一世上的岛屿数量。

实现细节

你需要实现下面的函数：

string process(string[][] a, int i, int j, int k, int n)

• $a$：一个 $3 \times 3$ 数组，表示正在被处理的子数组。特别说明，有 $a = h[i \dots i + 2][j \dots j + 2]$，这里 $a$ 中的每个元素均为长度恰好为 $100$ 的字符串，而且串中的字符为 $\texttt{0}$（ASCII 码 $48$）或 $\texttt{1}$（ASCII 码 $49$）。
• $i, j$：电脑当前正在处理的单元的行号和列号。
• $k$：当前阶段的序号。
• $n$：阶段总数，同时也是行星表面的大小，此时行星表面包含 $(2n + 1) \times (2n + 1)$ 个单元。
• 该函数应返回一个长度为 $100$ 的二进制表示字符串。返回值将保存在电脑存储器中的 $h[i][j]$ 处。
• $k = n - 1$ 时，是该函数的最后一次调用。在此次调用中，函数应以字符串的形式返回行星上的岛屿数量的二进制表示，其最低有效位对应下标 $0$ 处的字符（二进制字符串的首字符），次低有效位对应下标 $1$ 处的字符，以此类推。
• 该函数必须独立于任何的静态或全局变量，且其返回值应仅依赖于传递给该函数的参数。

每个测试用例包括 $T$ 个独立的场景（也就是说，不同的行星表面情形）。你的函数在每个场景上的行为，必须与这些场景的顺序无关，因为对同一场景的 process 函数调用可能不是连续发生的。但是，可以确保对每个场景，会按照题面所描述的顺序来调用函数 process。

此外，对每个测试用例，你的程序可能会同时运行多个实例。内存限制和 CPU 用时限制将施加在所有这些实例的总和上。任何故意在这些实例之间偷偷传递数据的行为，都将被认定为作弊，选手可能会因此被取消比赛资格。

【注】：洛谷暂不支持这种评测方式，我实现了一个洛谷支持的简易版本的交互库，但不能对传递数据进行有效限制，请各位自觉。

特别说明，在调用函数 process 时保存在静态或全局变量中的信息，不保证在下次调用时可以读出。

输入格式

评测程序示例读取如下格式的输入：

• 第 $1$ 行：$T$。
• 第 $i$ 个区块（$0 \le i \le T - 1$）：该区块表示第 $i$ 个场景。
  • 第 $1$ 行：$n$。
  • 第 $2 + j$ 行（$0 \le j \le 2 ⋅ n$）：$s[j][0]\ s[j][1]\ \dots\ s[j][2 \cdot n]$。

输出格式

评测程序示例将按照如下格式打印出结果：

• 第 $1 + i$ 行（$0 \le i \le T - 1$）：在第 $i$ 个场景上，函数 process 最后一次的返回值的十进制表示。

1
1
1 0 0
1 1 0
0 0 1

2

1
2
1 1 0 1 1
1 1 0 0 0
1 0 1 1 1
0 1 0 0 0
0 1 1 1 1

4

提示

例子

例 $1$

考虑 $n=1$ 的样例，其中 $s$ 如下所示：

'1' '0' '0'
'1' '1' '0'
'0' '0' '1'

在本例中，行星表面包括 $3 \times 3$ 个单元，其中有 $2$ 个岛屿。对函数 process 的调用至多只有 $1$ 个阶段。

在阶段 $0$，评测程序将调用函数 process 恰好一次：

process([["100","000","000"],["100","100","000"],["000","000","100"]],0,0,0,1)

注意这里仅展示了 $h$ 中每个元素的前 $3$ 位。

该函数应返回 $\texttt{0100}\dots$（省略的位全部为零），这里二进制的 $\dots 0010$ 等于十进制的 $2$。注意，这里省略了 $96$ 个零并用 $\dots$ 来代替。

例 $2$

考虑 $n=2$ 的样例，其中 $s$ 如下所示：

'1' '1' '0' '1' '1'
'1' '1' '0' '0' '0'
'1' '0' '1' '1' '1'
'0' '1' '0' '0' '0'
'0' '1' '1' '1' '1'

在本例中，行星表面包括 $5 \times 5$ 个单元，其中有 $4$ 个岛屿。对函数 process 的调用至多只有 $2$ 个阶段。

在阶段 $0$，评测程序将调用函数 process 恰好一次：

process([["100","100","000"],["100","100","000"],["100","000","100"]],0,0,0,2)
process([["100","000","100"],["100","000","000"],["000","100","100"]],0,1,0,2)
process([["000","100","100"],["000","000","000"],["100","100","100"]],0,2,0,2)
process([["100","100","000"],["100","000","100"],["000","100","000"]],1,0,0,2)
process([["100","000","000"],["000","100","100"],["100","000","000"]],1,1,0,2)
process([["000","000","000"],["100","100","100"],["000","000","000"]],1,2,0,2)
process([["100","000","100"],["000","100","000"],["000","100","100"]],2,0,0,2)
process([["000","100","100"],["100","000","000"],["100","100","100"]],2,1,0,2)
process([["100","100","100"],["000","000","000"],["100","100","100"]],2,2,0,2)

假定上面调用得到的返回值分别为 $\texttt{011},\texttt{000},\texttt{000},\texttt{111},\texttt{111},\texttt{011},\texttt{110},\texttt{010},\texttt{111}$，被省略的位均为零。因此，在阶段 $0$ 结束后，$h$ 将保存有如下的值：

"011", "000", "000", "100", "100"
"111", "111", "011", "000", "000"
"110", "010", "111", "100", "100"
"000", "100", "000", "000", "000"
"000", "100", "100", "100", "100"

在阶段 $1$，评测程序将调用函数 process 一次：

process([["011","000","000"],["111","111","011"],["110","010","111"]],0,0,1,2)

最后，本次函数调用应返回 $\texttt{0010000}\dots$（被省略的位均为零），这里二进制的 $\dots 0000100$ 等于十进制的 $4$。注意这里省略了 $93$ 个零并用 $\dots$ 来代替。

约束条件

• $1\le T\le 10$。
• $1\le n\le 20$。
• $s[i][j]$ 为 $\texttt{0}$（ASCII 码 $48$）或 $\texttt{1}$（ASCII 码 $49$）（对所有 $0\le i,j\le 2\cdot n$）。
• $h[i][j]$ 的长度恰好为 $100$（对所有 $0\le i,j\le 2\cdot n$）。
• $h[i][j]$ 中的每个字符均为 $\texttt{0}$（ASCII 码 $48$）或 $\texttt{1}$（ASCII 码 $49$）（对所有 $0\le i,j\le 2\cdot n$）。

对函数 process 的每次调用，都有：

• $0\le k\le n-1$。
• $0\le i,j\le 2\cdot (n-k-1)$。

子任务

1. （$6$ 分）$n\le 2$。
2. （$8$ 分）$n\le 4$。
3. （$7$ 分）$n\le 6$。
4. （$8$ 分）$n\le 8$。
5. （$7$ 分）$n\le 10$。
6. （$8$ 分）$n\le 12$。
7. （$10$ 分）$n\le 14$。
8. （$24$ 分）$n\le 16$。
9. （$11$ 分）$n\le 18$。
10. （$11$ 分）$n\le 20$。