#P8303. [CoE R4 C] 网格
[CoE R4 C] 网格
题目描述
这是一道交互题。
有一张 个点的无向无权图。
这张图有一个特殊性质:存在一个点 到正整数对 的一一对应关系,使得 ,且点 间存在边当且仅当 对应的数对 满足 。换而言之,这张图和 行 列的网格图同构。
现在,你要通过一些询问还原这张图的结构。每次询问时,你需要给定一个点 。询问的返回值是一个长为 的数组 ,表示点 间的最短路径所经过的边数。
请你使用不超过 次询问,还原出这张图的结构。
交互格式
本题有多组数据。
首先输入一个整数 ,表示数据组数。
对于每组数据:
- 首先输入一个整数 ,表示图的点数。
- 接下来,你可以执行一些询问。对于每次询问,输出一个整数 ,为你询问的点。然后,输入 个整数 ,为询问的返回值。
- 当你确定答案后,输出一个整数 ,然后输出答案。
在输出答案时:
- 第一行输出两个整数 ;
- 接下来,输出 行 列整数,为你还原的对应关系。第 行 列的数为 对应的编号。
如果有多个答案,你可以输出任意一个。一个答案是正确的,当且仅当它和标准答案无法被任何询问区分:也就是,在这两个答案对应的网格图中,任意点对间的最短路径所经过的边数都是相同的。
请注意:在每次执行询问或者输出答案后,你应该清空缓冲区:
- 在 C++ 中,使用
fflush(stdout)或cout.flush()。 - 在 Java 中,使用
System.out.flush()。 - 在 Python 中,使用
stdout.flush()。 - 在 Pascal 中,使用
flush(output)。 - 对于其他语言,请自行查阅对应语言的帮助文档。
输入格式
见「交互格式」。
输出格式
见「交互格式」。
1
6
0 2 2 3 1 1
2 0 2 1 1 3
2 2 0 1 1 1
3 1 1 0 2 2
1 1 1 2 0 2
1 3 1 2 2 0
1
2
3
4
5
6
0
2 3
2 5 1
4 3 6
2
1
2
1 0
0
1 1
1
2
0
2 1
1
2
提示
样例 解释
对于样例,以下 行 列的网格图也是正确的输出。
3 2
4 2
3 5
6 1
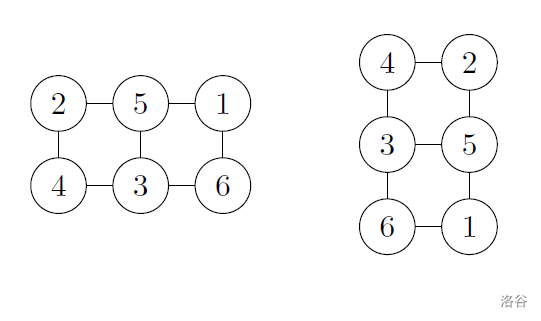
左边是样例对应的网格图,右边是以上输出对应的网格图。
评分标准
对于一个子任务,令 为你在这个子任务的所有测试数据中的最大询问次数。
如果交互的格式不合法,运行超出了时间限制,或者你的答案不正确,或者 ,你的得分为 。
否则,对于子任务 ,你得满分;对于子任务 ,你的分数由下表给出:
| 条件 | 分数 |
|---|---|
数据规模
本题采用捆绑测试。
| 子任务 | 分值 | 特殊性质 | ||
|---|---|---|---|---|
| 无 | ||||
| 存在解使得 | ||||
| 存在解使得 | ||||
| 无 | ||||
对于所有数据,保证 ,,。
在部分测试数据中,交互器是自适应的。也就是,图的结构可能会根据你的询问而变化。但是可以保证:在每次询问之后,存在至少一个答案符合当前所有询问的返回值。
