题目描述

给定一个无限大的棋盘（可以看做平面直角坐标系）和黑白子各 $n$ 颗，要求将黑白子不重叠地摆在棋盘的整点上，使得恰好存在 $n$ 条直线使得：

• 其穿过且仅穿过黑白子共 4 颗。

• 其按顺序穿过黑，白，白，黑子。

给出任意一种方案即可。

输入格式

输入数据仅一行，为题目中所述的 $n$。

输出格式

如果无法构造出方案，则输出 NO。

否则输出 $2n+1$ 行：第一行输出 YES。第 $2\sim n+1$ 行每行两个整数，为白子坐标 $x_i,y_i$。第 $n+2\sim 2n+1$ 行每行两个整数，为黑子坐标 $x_j,y_j$。

你需要保证 $-5\times 10^5\le x_i,y_i,x_j,y_j\le 5\times 10^5$。

1

NO

7

YES
2 4
2 6
4 6
5 4
6 4
6 2
4 2
0 6
2 8
6 6
8 2
6 0
3 0
2 2

提示

【样例解释】

样例 2 解释：（输出按顺序为点 $A\sim N$（点 $A\sim G$ 为白子，点 $H\sim N$ 为黑子），直线如图所示）。

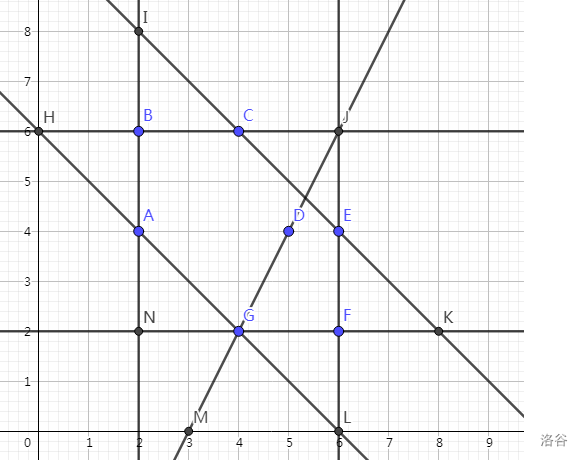
【数据范围】

本题采用捆绑测试。

• Subtask 1（10 pts）：$n\equiv 0 \pmod{7}$；
• Subtask 2（20 pts）：$40\le n\le 400$；
• Subtask 3（30 pts）：$1\le n\le 9$；
• Subtask 4（40 pts）：无特殊限制。

对于 $100\%$ 的数据，$1\le n\le 10^3$。

SPJ地址

使用方法：编译为 checker.exe 后命令行同一目录下输入 checker.exe chessboard.in chessboard.out chessboard.ans

需要搭配 testlib.h 一起使用，testlib下载地址。

如果发现 SPJ 出锅了请找出题人。